Fuzzy C-Mean Clustering#
Konsep dasar Fuzzy C-Mean Clustering#
Fuzzy C-Means (FCM) adalah salah satu metode clustering yang memungkinkan satu data menjadi anggota lebih dari satu cluster dengan derajat keanggotaan tertentu (nilai antara 0 dan 1). Berbeda dengan k-means yang bersifat hard clustering (anggota hanya milik satu cluster), FCM bersifat soft clustering.
Berbeda dengan metode K-Means yang bersifat tegas, FCM memungkinkan fleksibilitas dalam menentukan klaster karena setiap data memiliki nilai keanggotaan terhadap semua klaster yang totalnya berjumlah 1.
Tujuan utama dari algoritma ini adalah meminimalkan fungsi objektif yang mempertimbangkan jarak data terhadap pusat klaster dan tingkat keanggotaannya. Algoritma ini bekerja secara iteratif dengan menghitung pusat klaster dan memperbarui nilai keanggotaan hingga nilai-nilai tersebut stabil atau konvergen.
Keunggulan FCM terletak pada kemampuannya menangani data yang tidak memiliki batas klaster yang jelas, sehingga cocok untuk aplikasi dunia nyata seperti segmentasi citra atau analisis perilaku konsumen. Namun, algoritma ini juga memiliki kelemahan, seperti sensitif terhadap inisialisasi awal dan lambat saat digunakan pada data dalam jumlah besar. Selain itu, parameter fuzziness (biasanya disimbolkan dengan ๐ m) memengaruhi tingkat โkaburโ-nya keanggotaan, dan harus ditentukan secara tepat agar hasil klasterisasi optimal.
Algoritma Fuzzy C-Mean Clustering#
Algoritma Fuzzy C-Means (FCM) adalah metode clustering yang menggunakan konsep fuzzy, di mana setiap data dapat menjadi anggota lebih dari satu cluster dengan derajat ketebalan yang berbeda, bernilai antara 0 sampai 1. Algoritma ini memungkinkan data memiliki keseluruhan parsial pada beberapa cluster, berbeda dengan metode clustering keras seperti K-Means yang hanya mengelompokkan data ke satu cluster saja.
Langkah-langkah Fuzzy C-Mean Clustering#
Menentukan jumlah cluster (c) yang diinginkan.
Inisialisasi matriks derajat keanggotaan (U) secara acak, di mana setiap baris mewakili data dan setiap kolom mewakili cluster. Nilai derajat keanggotaan tiap data pada semua cluster harus berjumlah 1.
Menghitung pusat cluster (centroid) menggunakan rumus rata-rata berbobot, di mana bobotnya adalah derajat pengumpulan data yang dipangkatkan dengan parameter fuzziness M>1.
Memperbarui derajat pengumpulan (U) berdasarkan jarak data ke pusat cluster yang baru dihitung, sehingga data yang lebih dekat ke pusat cluster memiliki derajat keanggotaan lebih tinggi.
Menghitung fungsi tujuan yang mengukur total jarak berbobot antara data dan pusat cluster. Fungsi ini diminimasi untuk mendapatkan hasil clustering terbaik.
Iterasi langkah 3 sampai 5 dilakukan sampai perubahan fungsi tujuan atau perubahan derajat pengumpulan lebih kecil dari nilai toleransi yang telah ditentukan, atau sampai mencapai jumlah iterasi maksimal.
Fungsi Objektif Fuzzy C-Means
\[
J_m = \sum_{i=1}^{n} \sum_{j=1}^{c} u_{ij}^m \cdot \|x_i - c_j\|^2
\]
Keterangan:
( J_m ) : Fungsi objektif yang diminimalkan
( n ) : Jumlah data
( c ) : Jumlah klaster
( u_{ij} ) : Derajat keanggotaan data ke-(i) terhadap klaster ke-(j)
( m ) : Parameter fuzziness (biasanya ( m = 2 ))
( x_i ) : Data ke-(i)
( c_j ) : Pusat klaster ke-(j)
( |x_i - c_j| ) : Jarak antara data ke-(i) dan pusat klaster ke-(j) (biasanya Euclidean distance)
Update derajat keanggotaaan#
Rumus Update Derajat Keanggotaan (Membership Update)
\[
u_{ij} = \frac{1}{\sum_{k=1}^{c} \left( \frac{\|x_i - c_j\|}{\|x_i - c_k\|} \right)^{\frac{2}{m - 1}}}
\]
Keterangan:
( u_{ij} ) : Derajat keanggotaan data ke-(i) terhadap klaster ke-(j)
( c ) : Jumlah klaster
( x_i ) : Data ke-(i)
( c_j ) : Pusat klaster ke-(j)
( |x_i - c_j| ) : Jarak antara data ke-(i) dan pusat klaster ke-(j)
( m ) : Parameter fuzziness (biasanya ( m = 2 ))
Update pusat Cluster#
Rumus Update Pusat Klaster
\[
c_j = \frac{\sum_{i=1}^{n} u_{ij}^m \cdot x_i}{\sum_{i=1}^{n} u_{ij}^m}
\]
Keterangan:
( c_j ) : Pusat klaster ke-(j)
( n ) : Jumlah data
( u_{ij} ) : Derajat keanggotaan data ke-(i) terhadap klaster ke-(j)
( m ) : Parameter fuzziness (biasanya ( m = 2 ))
( x_i ) : Data ke-(i)
Fuzzy C-Means Clustering (Manual)#
๐ Data
xi |
x1 |
x2 |
|---|---|---|
1 |
1 |
2 |
2 |
2 |
3 |
3 |
3 |
4 |
4 |
6 |
7 |
5 |
7 |
8 |
๐งฎ Matriks Keanggotaan Awal (U)
xi |
(\mu_{i1}) (dc1) |
(\mu_{i2}) (dc2) |
|---|---|---|
1 |
0.3 |
0.7 |
2 |
0.2 |
0.8 |
3 |
0.4 |
0.6 |
4 |
0.7 |
0.3 |
5 |
0.1 |
0.9 |
Dengan:
Jumlah data: ( n = 5 )
Jumlah cluster: ( c = 2 )
Fuzzifier: ( m = 2 )
๐ Rumus Centroid
Centroid untuk cluster ke-( j ) adalah:
\[
v_j = \frac{\sum_{i=1}^{n} \left( \mu_{ij} \right)^m x_i}{\sum_{i=1}^{n} \left( \mu_{ij} \right)^m}
\]
๐ข Perhitungan Centroid Cluster 1 ((v_1))
Langkah 1: Hitung $\(( (\mu_{i1})^2 )\)$
\[
\mu_{i1}^2 = \{0.3^2, 0.2^2, 0.4^2, 0.7^2, 0.1^2\} = \{0.09, 0.04, 0.16, 0.49, 0.01\}
\]
Langkah 2: Hitung $\(( v_{1x1} )\)$
\[
v_{1x1} = \frac{0.09 \cdot 1 + 0.04 \cdot 2 + 0.16 \cdot 3 + 0.49 \cdot 6 + 0.01 \cdot 7}{0.09 + 0.04 + 0.16 + 0.49 + 0.01}
\]
\[
= \frac{0.09 + 0.08 + 0.48 + 2.94 + 0.07}{0.79} = \frac{3.66}{0.79} \approx 4.63
\]
Langkah 3: Hitung $\(( v_{1x2} )\)$
\[
v_{1x2} = \frac{0.09 \cdot 2 + 0.04 \cdot 3 + 0.16 \cdot 4 + 0.49 \cdot 7 + 0.01 \cdot 8}{0.79}
\]
\[
= \frac{0.18 + 0.12 + 0.64 + 3.43 + 0.08}{0.79} = \frac{4.45}{0.79} \approx 5.63
\]
โ Hasil Centroid 1
\[
v_1 \approx (4.63,\ 5.63)
\]
๐งฎ Perhitungan Centroid Cluster 2 ($\((v_2))\)$
Langkah 1: Hitung $\(( (\mu_{i2})^2 )\)$
\[
\mu_{i2}^2 = \{0.7^2, 0.8^2, 0.6^2, 0.3^2, 0.9^2\} = \{0.49, 0.64, 0.36, 0.09, 0.81\}
\]
Langkah 2: Hitung $\(( v_{2x1} )\)$
\[
v_{2x1} = \frac{0.49 \cdot 1 + 0.64 \cdot 2 + 0.36 \cdot 3 + 0.09 \cdot 6 + 0.81 \cdot 7}{0.49 + 0.64 + 0.36 + 0.09 + 0.81}
\]
\[
= \frac{0.49 + 1.28 + 1.08 + 0.54 + 5.67}{2.39} = \frac{9.06}{2.39} \approx 3.79
\]
Langkah 3: Hitung $\(( v_{2x2} )\)$
\[
v_{2x2} = \frac{0.49 \cdot 2 + 0.64 \cdot 3 + 0.36 \cdot 4 + 0.09 \cdot 7 + 0.81 \cdot 8}{2.39}
\]
\[
= \frac{0.98 + 1.92 + 1.44 + 0.63 + 6.48}{2.39} = \frac{11.45}{2.39} \approx 4.79
\]
โ Hasil Centroid 2
\[
v_2 \approx (3.79,\ 4.79)
\]
๐งพ Ringkasan Centroid Iterasi 1
- \[( v_1 = (4.63,\ 5.63) )\]
- \[( v_2 = (3.79,\ 4.79) )\]
Langkah Selanjutnya: Update Keanggotaan dan Jarak#
Hitung Jarak Euclidean dari setiap data ke centroid
Rumus jarak data $\((x_i = (x_{i1}, x_{i2}) )\)\( ke centroid cluster \)\((v_j = (v_{j1}, v_{j2}) )\)$ :
\[
d_{ij} = \sqrt{(x_{i1} - v_{j1})^2 + (x_{i2} - v_{j2})^2}
\]
Contoh Hitung Jarak untuk Data ke-1 ( (1,2) )
Dengan centroid cluster:
\[
v_1 = (4.63, 5.63), \quad v_2 = (3.79, 4.79)
\]
Jarak ke cluster 1:
\[
d_{11} = \sqrt{(1 - 4.63)^2 + (2 - 5.63)^2} = \sqrt{(-3.63)^2 + (-3.63)^2} = \sqrt{13.18 + 13.18} = \sqrt{26.36} \approx 5.13
\]
Jarak ke cluster 2:
\[
d_{12} = \sqrt{(1 - 3.79)^2 + (2 - 4.79)^2} = \sqrt{(-2.79)^2 + (-2.79)^2} = \sqrt{7.78 + 7.78} = \sqrt{15.56} \approx 3.94
\]
Update Keanggotaan Baru
Rumus update keanggotaan:
\[
\mu_{ij} = \frac{1}{\sum_{k=1}^{c} \left( \frac{d_{ij}}{d_{ik}} \right)^{\frac{2}{m-1}}}
\]
Misalkan ( m=2 ) dan ( c=2 ), maka untuk data ke-1 cluster 1:
\[
\mu_{11} = \frac{1}{\left( \frac{d_{11}}{d_{11}} \right)^2 + \left( \frac{d_{11}}{d_{12}} \right)^2} = \frac{1}{1 + \left( \frac{5.13}{3.94} \right)^2} = \frac{1}{1 + 1.69} = \frac{1}{2.69} \approx 0.37
\]
Untuk cluster 2:
\[
\mu_{12} = \frac{1}{\left( \frac{d_{12}}{d_{11}} \right)^2 + \left( \frac{d_{12}}{d_{12}} \right)^2} = \frac{1}{\left( \frac{3.94}{5.13} \right)^2 + 1} = \frac{1}{0.59 + 1} = \frac{1}{1.59} \approx 0.63
\]
Ulangi untuk semua data dan cluster
Lakukan perhitungan jarak dan update keanggotaan ini untuk seluruh data dan cluster.
Cek konvergensi
Jika perubahan keanggotaan sudah kecil, proses berhenti. Jika belum, ulangi hitung centroid baru dan update keanggotaan sampai konvergen.
Data dan Keanggotaan Fuzzy#
Data \((x_i)\) |
\((x_1)\) |
\((x_2) \) |
\((\mu_{i1}) \) |
\((\mu_{i2}) \) |
|---|---|---|---|---|
1 |
1 |
2 |
0.3 |
0.7 |
2 |
2 |
3 |
0.2 |
0.8 |
3 |
3 |
4 |
0.4 |
0.6 |
4 |
6 |
7 |
0.7 |
0.3 |
5 |
7 |
8 |
0.1 |
0.9 |
Menentukan Cluster Akhir
Cluster akhir untuk data $\((x_i)\)$ adalah cluster dengan nilai keanggotaan fuzzy terbesar:
\[
\text{Cluster akhir untuk data } x_i = \arg\max_{j} \mu_{ij}
\]
Hasil Perhitungan Cluster Akhir
Data \((x_i)\) |
\((\mu_{i1})\) |
\((\mu_{i2})\) |
Cluster Akhir |
|---|---|---|---|
1 |
0.3 |
0.7 |
2 |
2 |
0.2 |
0.8 |
2 |
3 |
0.4 |
0.6 |
2 |
4 |
0.7 |
0.3 |
1 |
5 |
0.1 |
0.9 |
2 |
Implementasi Python serta Menampilkan nilai pusat cluster,keanggotaan setiap iterasi dan hitung fungsi objektif setiap iterasi#
import numpy as np
# Data (x1, x2)
data = np.array([
[1, 2],
[2, 3],
[3, 4],
[6, 7],
[7, 8]
], dtype=float)
# Keanggotaan fuzzy mu_ij untuk 2 cluster
U = np.array([
[0.3, 0.7],
[0.2, 0.8],
[0.4, 0.6],
[0.7, 0.3],
[0.1, 0.9]
], dtype=float)
m = 2.0 # derajat fuzziness
epsilon = 0.01
max_iter = 100
# Update centroid untuk data 2D
def update_centroids(U, data, m):
um = U ** m # (n, c)
centroids = np.dot(um.T, data) / um.sum(axis=0)[:, None] # (c, 2)
return centroids
# Update keanggotaan fuzzy untuk data 2D
def update_membership(data, centroids, m):
n = data.shape[0]
c = centroids.shape[0]
new_U = np.zeros((n, c))
for i in range(n):
for j in range(c):
d_ij = np.linalg.norm(data[i] - centroids[j]) + 1e-10
denom = sum([
(d_ij / (np.linalg.norm(data[i] - centroids[k]) + 1e-10)) ** (2 / (m - 1))
for k in range(c)
])
new_U[i, j] = 1 / denom
return new_U
# Fungsi objektif untuk data 2D
def objective_function(U, data, centroids, m):
J = 0
for i in range(len(data)):
for j in range(len(centroids)):
dist_sq = np.linalg.norm(data[i] - centroids[j]) ** 2
J += (U[i][j] ** m) * dist_sq
return J
# Iterasi algoritma Fuzzy C-Means
for iteration in range(max_iter):
centroids = update_centroids(U, data, m)
new_U = update_membership(data, centroids, m)
J = objective_function(new_U, data, centroids, m)
delta_U = np.max(np.abs(new_U - U))
print(f"Iterasi {iteration + 1}")
print("Centroid:\n", np.round(centroids, 4))
print("Matriks Keanggotaan (U):\n", np.round(new_U, 4))
print("Fungsi Objektif (J):", round(J, 4))
print("Perubahan Maksimum Delta U:", round(delta_U, 6))
print("-" * 40)
if delta_U < epsilon:
print(f"โ
Konvergen pada iterasi ke-{iteration + 1}")
break
U = new_U
else:
print("โ Tidak konvergen hingga iterasi maksimum.")
Iterasi 1
Centroid:
[[4.6329 5.6329]
[3.7908 4.7908]]
Matriks Keanggotaan (U):
[[0.3711 0.6289]
[0.3163 0.6837]
[0.19 0.81 ]
[0.7231 0.2769]
[0.6476 0.3524]]
Fungsi Objektif (J): 25.155
Perubahan Maksimum Delta U: 0.54765
----------------------------------------
Iterasi 2
Centroid:
[[5.3606 6.3606]
[2.6908 3.6908]]
Matriks Keanggotaan (U):
[[0.1307 0.8693]
[0.0405 0.9595]
[0.0169 0.9831]
[0.964 0.036 ]
[0.8736 0.1264]]
Fungsi Objektif (J): 11.5579
Perubahan Maksimum Delta U: 0.275753
----------------------------------------
Iterasi 3
Centroid:
[[6.3916 7.3916]
[2.1113 3.1113]]
Matriks Keanggotaan (U):
[[4.070e-02 9.593e-01]
[6.000e-04 9.994e-01]
[6.430e-02 9.357e-01]
[9.900e-01 1.000e-02]
[9.848e-01 1.520e-02]]
Fungsi Objektif (J): 4.9047
Perubahan Maksimum Delta U: 0.111187
----------------------------------------
Iterasi 4
Centroid:
[[6.4853 7.4853]
[1.9846 2.9846]]
Matriks Keanggotaan (U):
[[0.0312 0.9688]
[0. 1. ]
[0.0782 0.9218]
[0.9856 0.0144]
[0.9896 0.0104]]
Fungsi Objektif (J): 4.7681
Perubahan Maksimum Delta U: 0.013981
----------------------------------------
Iterasi 5
Centroid:
[[6.4883 7.4883]
[1.9686 2.9686]]
Matriks Keanggotaan (U):
[[0.0302 0.9698]
[0. 1. ]
[0.0804 0.9196]
[0.9855 0.0145]
[0.9898 0.0102]]
Fungsi Objektif (J): 4.7665
Perubahan Maksimum Delta U: 0.002158
----------------------------------------
โ
Konvergen pada iterasi ke-5
Implementasi Fuzzy C-Means Clustering Untuk data Iris (3Cluster)#
inisialisasi Data Iris dan Parameter#
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
# Fungsi ambil data Iris dan atur ulang kolom
def get_iris_data():
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df["class"] = pd.Categorical.from_codes(iris.target, iris.target_names)
df["id"] = df.index + 1 # ID dimulai dari 1
# Susun ulang kolom: id, class, lalu fitur
columns_order = ["id", "class"] + iris.feature_names
df = df[columns_order]
return df
# Ambil data
df_iris = get_iris_data()
# Muat data Iris
iris = load_iris()
X = iris.data # Semua fitur: shape (150, 4)
feature_names = iris.feature_names
# Cetak tanpa indeks
print(df_iris.to_string(index=False))
# Parameter FCM
k = 3 # Jumlah cluster
m = 2.0 # Derajat fuzziness
max_iter = 100 # Maksimum iterasi
epsilon = 0.01 # Ambang batas konvergensi
n = X.shape[0] # Jumlah data (150)
d = X.shape[1] # Jumlah fitur (4)
# Inisialisasi keanggotaan acak (jumlah baris = data, kolom = cluster)
U = np.random.dirichlet(np.ones(k), size=n)
print()
# Cetak semua parameter
print("๐ Parameter FCM:")
print(f"Jumlah data (n) : {n}")
print(f"Jumlah fitur (d) : {d} ({', '.join(feature_names)})")
print(f"Jumlah cluster (k) : {k}")
print(f"Fuzziness (m) : {m}")
print(f"Maksimum iterasi : {max_iter}")
print(f"Ambang konvergensi : {epsilon}")
print(f"Shape matriks keanggotaan U: {U.shape}")
id class sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
1 setosa 5.1 3.5 1.4 0.2
2 setosa 4.9 3.0 1.4 0.2
3 setosa 4.7 3.2 1.3 0.2
4 setosa 4.6 3.1 1.5 0.2
5 setosa 5.0 3.6 1.4 0.2
6 setosa 5.4 3.9 1.7 0.4
7 setosa 4.6 3.4 1.4 0.3
8 setosa 5.0 3.4 1.5 0.2
9 setosa 4.4 2.9 1.4 0.2
10 setosa 4.9 3.1 1.5 0.1
11 setosa 5.4 3.7 1.5 0.2
12 setosa 4.8 3.4 1.6 0.2
13 setosa 4.8 3.0 1.4 0.1
14 setosa 4.3 3.0 1.1 0.1
15 setosa 5.8 4.0 1.2 0.2
16 setosa 5.7 4.4 1.5 0.4
17 setosa 5.4 3.9 1.3 0.4
18 setosa 5.1 3.5 1.4 0.3
19 setosa 5.7 3.8 1.7 0.3
20 setosa 5.1 3.8 1.5 0.3
21 setosa 5.4 3.4 1.7 0.2
22 setosa 5.1 3.7 1.5 0.4
23 setosa 4.6 3.6 1.0 0.2
24 setosa 5.1 3.3 1.7 0.5
25 setosa 4.8 3.4 1.9 0.2
26 setosa 5.0 3.0 1.6 0.2
27 setosa 5.0 3.4 1.6 0.4
28 setosa 5.2 3.5 1.5 0.2
29 setosa 5.2 3.4 1.4 0.2
30 setosa 4.7 3.2 1.6 0.2
31 setosa 4.8 3.1 1.6 0.2
32 setosa 5.4 3.4 1.5 0.4
33 setosa 5.2 4.1 1.5 0.1
34 setosa 5.5 4.2 1.4 0.2
35 setosa 4.9 3.1 1.5 0.2
36 setosa 5.0 3.2 1.2 0.2
37 setosa 5.5 3.5 1.3 0.2
38 setosa 4.9 3.6 1.4 0.1
39 setosa 4.4 3.0 1.3 0.2
40 setosa 5.1 3.4 1.5 0.2
41 setosa 5.0 3.5 1.3 0.3
42 setosa 4.5 2.3 1.3 0.3
43 setosa 4.4 3.2 1.3 0.2
44 setosa 5.0 3.5 1.6 0.6
45 setosa 5.1 3.8 1.9 0.4
46 setosa 4.8 3.0 1.4 0.3
47 setosa 5.1 3.8 1.6 0.2
48 setosa 4.6 3.2 1.4 0.2
49 setosa 5.3 3.7 1.5 0.2
50 setosa 5.0 3.3 1.4 0.2
51 versicolor 7.0 3.2 4.7 1.4
52 versicolor 6.4 3.2 4.5 1.5
53 versicolor 6.9 3.1 4.9 1.5
54 versicolor 5.5 2.3 4.0 1.3
55 versicolor 6.5 2.8 4.6 1.5
56 versicolor 5.7 2.8 4.5 1.3
57 versicolor 6.3 3.3 4.7 1.6
58 versicolor 4.9 2.4 3.3 1.0
59 versicolor 6.6 2.9 4.6 1.3
60 versicolor 5.2 2.7 3.9 1.4
61 versicolor 5.0 2.0 3.5 1.0
62 versicolor 5.9 3.0 4.2 1.5
63 versicolor 6.0 2.2 4.0 1.0
64 versicolor 6.1 2.9 4.7 1.4
65 versicolor 5.6 2.9 3.6 1.3
66 versicolor 6.7 3.1 4.4 1.4
67 versicolor 5.6 3.0 4.5 1.5
68 versicolor 5.8 2.7 4.1 1.0
69 versicolor 6.2 2.2 4.5 1.5
70 versicolor 5.6 2.5 3.9 1.1
71 versicolor 5.9 3.2 4.8 1.8
72 versicolor 6.1 2.8 4.0 1.3
73 versicolor 6.3 2.5 4.9 1.5
74 versicolor 6.1 2.8 4.7 1.2
75 versicolor 6.4 2.9 4.3 1.3
76 versicolor 6.6 3.0 4.4 1.4
77 versicolor 6.8 2.8 4.8 1.4
78 versicolor 6.7 3.0 5.0 1.7
79 versicolor 6.0 2.9 4.5 1.5
80 versicolor 5.7 2.6 3.5 1.0
81 versicolor 5.5 2.4 3.8 1.1
82 versicolor 5.5 2.4 3.7 1.0
83 versicolor 5.8 2.7 3.9 1.2
84 versicolor 6.0 2.7 5.1 1.6
85 versicolor 5.4 3.0 4.5 1.5
86 versicolor 6.0 3.4 4.5 1.6
87 versicolor 6.7 3.1 4.7 1.5
88 versicolor 6.3 2.3 4.4 1.3
89 versicolor 5.6 3.0 4.1 1.3
90 versicolor 5.5 2.5 4.0 1.3
91 versicolor 5.5 2.6 4.4 1.2
92 versicolor 6.1 3.0 4.6 1.4
93 versicolor 5.8 2.6 4.0 1.2
94 versicolor 5.0 2.3 3.3 1.0
95 versicolor 5.6 2.7 4.2 1.3
96 versicolor 5.7 3.0 4.2 1.2
97 versicolor 5.7 2.9 4.2 1.3
98 versicolor 6.2 2.9 4.3 1.3
99 versicolor 5.1 2.5 3.0 1.1
100 versicolor 5.7 2.8 4.1 1.3
101 virginica 6.3 3.3 6.0 2.5
102 virginica 5.8 2.7 5.1 1.9
103 virginica 7.1 3.0 5.9 2.1
104 virginica 6.3 2.9 5.6 1.8
105 virginica 6.5 3.0 5.8 2.2
106 virginica 7.6 3.0 6.6 2.1
107 virginica 4.9 2.5 4.5 1.7
108 virginica 7.3 2.9 6.3 1.8
109 virginica 6.7 2.5 5.8 1.8
110 virginica 7.2 3.6 6.1 2.5
111 virginica 6.5 3.2 5.1 2.0
112 virginica 6.4 2.7 5.3 1.9
113 virginica 6.8 3.0 5.5 2.1
114 virginica 5.7 2.5 5.0 2.0
115 virginica 5.8 2.8 5.1 2.4
116 virginica 6.4 3.2 5.3 2.3
117 virginica 6.5 3.0 5.5 1.8
118 virginica 7.7 3.8 6.7 2.2
119 virginica 7.7 2.6 6.9 2.3
120 virginica 6.0 2.2 5.0 1.5
121 virginica 6.9 3.2 5.7 2.3
122 virginica 5.6 2.8 4.9 2.0
123 virginica 7.7 2.8 6.7 2.0
124 virginica 6.3 2.7 4.9 1.8
125 virginica 6.7 3.3 5.7 2.1
126 virginica 7.2 3.2 6.0 1.8
127 virginica 6.2 2.8 4.8 1.8
128 virginica 6.1 3.0 4.9 1.8
129 virginica 6.4 2.8 5.6 2.1
130 virginica 7.2 3.0 5.8 1.6
131 virginica 7.4 2.8 6.1 1.9
132 virginica 7.9 3.8 6.4 2.0
133 virginica 6.4 2.8 5.6 2.2
134 virginica 6.3 2.8 5.1 1.5
135 virginica 6.1 2.6 5.6 1.4
136 virginica 7.7 3.0 6.1 2.3
137 virginica 6.3 3.4 5.6 2.4
138 virginica 6.4 3.1 5.5 1.8
139 virginica 6.0 3.0 4.8 1.8
140 virginica 6.9 3.1 5.4 2.1
141 virginica 6.7 3.1 5.6 2.4
142 virginica 6.9 3.1 5.1 2.3
143 virginica 5.8 2.7 5.1 1.9
144 virginica 6.8 3.2 5.9 2.3
145 virginica 6.7 3.3 5.7 2.5
146 virginica 6.7 3.0 5.2 2.3
147 virginica 6.3 2.5 5.0 1.9
148 virginica 6.5 3.0 5.2 2.0
149 virginica 6.2 3.4 5.4 2.3
150 virginica 5.9 3.0 5.1 1.8
๐ Parameter FCM:
Jumlah data (n) : 150
Jumlah fitur (d) : 4 (sepal length (cm), sepal width (cm), petal length (cm), petal width (cm))
Jumlah cluster (k) : 3
Fuzziness (m) : 2.0
Maksimum iterasi : 100
Ambang konvergensi : 0.01
Shape matriks keanggotaan U: (150, 3)
Inisialisasi derajat Keanggotaan#
# Tambahkan ID ke matriks keanggotaan dan pindahkan ke kolom paling kiri
df_U = pd.DataFrame(U, columns=[f"Cluster_{i+1}" for i in range(k)])
df_U.insert(0, "id", df_U.index + 1) # ID dimulai dari 1
print("\n=== Matriks Keanggotaan Awal (U) ===")
print(df_U.to_string(index=False))
=== Matriks Keanggotaan Awal (U) ===
id Cluster_1 Cluster_2 Cluster_3
1 0.574412 0.329177 0.096411
2 0.622818 0.003090 0.374092
3 0.793289 0.154021 0.052691
4 0.721897 0.262183 0.015920
5 0.237387 0.006698 0.755915
6 0.691543 0.099814 0.208643
7 0.270446 0.110048 0.619506
8 0.308654 0.349983 0.341363
9 0.485916 0.393920 0.120164
10 0.394279 0.012365 0.593355
11 0.031279 0.534138 0.434583
12 0.649548 0.040930 0.309522
13 0.109715 0.342316 0.547969
14 0.346280 0.092905 0.560815
15 0.289032 0.293160 0.417808
16 0.014018 0.006482 0.979499
17 0.011534 0.185476 0.802990
18 0.658425 0.019270 0.322305
19 0.861307 0.130478 0.008215
20 0.138046 0.400846 0.461108
21 0.259460 0.438086 0.302454
22 0.229246 0.734431 0.036322
23 0.554417 0.138894 0.306689
24 0.069906 0.739319 0.190774
25 0.498388 0.043270 0.458341
26 0.648738 0.240543 0.110719
27 0.571788 0.223660 0.204552
28 0.105409 0.509237 0.385354
29 0.171179 0.225515 0.603305
30 0.730434 0.133952 0.135614
31 0.458121 0.225401 0.316478
32 0.285006 0.361358 0.353636
33 0.798821 0.029676 0.171503
34 0.436740 0.307818 0.255443
35 0.483299 0.120235 0.396466
36 0.077839 0.543554 0.378606
37 0.282188 0.368507 0.349305
38 0.568917 0.194597 0.236486
39 0.272549 0.126805 0.600646
40 0.259176 0.632100 0.108724
41 0.078251 0.895655 0.026095
42 0.171762 0.324628 0.503609
43 0.119233 0.367302 0.513466
44 0.207559 0.045783 0.746658
45 0.547287 0.437356 0.015357
46 0.412076 0.229253 0.358671
47 0.740766 0.180097 0.079136
48 0.389121 0.372565 0.238315
49 0.323536 0.555380 0.121084
50 0.032808 0.465875 0.501317
51 0.279892 0.599527 0.120581
52 0.674084 0.053665 0.272252
53 0.160392 0.110162 0.729446
54 0.174562 0.374906 0.450532
55 0.324452 0.297909 0.377639
56 0.297597 0.490553 0.211851
57 0.468503 0.491791 0.039707
58 0.815846 0.165350 0.018805
59 0.343843 0.394435 0.261722
60 0.266116 0.617332 0.116552
61 0.355864 0.345029 0.299107
62 0.320459 0.321352 0.358188
63 0.552846 0.064042 0.383112
64 0.567824 0.282421 0.149755
65 0.334427 0.274933 0.390641
66 0.189939 0.485137 0.324924
67 0.149970 0.846513 0.003517
68 0.553240 0.098366 0.348393
69 0.547682 0.237924 0.214393
70 0.215000 0.526194 0.258807
71 0.172184 0.700410 0.127406
72 0.035419 0.302060 0.662521
73 0.467017 0.242173 0.290810
74 0.073391 0.014931 0.911678
75 0.510350 0.221146 0.268504
76 0.872608 0.068633 0.058760
77 0.465463 0.473769 0.060768
78 0.721837 0.251682 0.026481
79 0.612173 0.308244 0.079582
80 0.197470 0.590501 0.212028
81 0.516019 0.315531 0.168449
82 0.206694 0.148127 0.645179
83 0.083906 0.769467 0.146627
84 0.350838 0.075919 0.573244
85 0.249252 0.507090 0.243658
86 0.202738 0.439436 0.357826
87 0.054068 0.659078 0.286854
88 0.031864 0.828931 0.139205
89 0.019227 0.269716 0.711057
90 0.298620 0.400313 0.301067
91 0.471159 0.323464 0.205377
92 0.102249 0.648820 0.248931
93 0.511498 0.142388 0.346114
94 0.383850 0.382515 0.233635
95 0.086031 0.695975 0.217994
96 0.045359 0.420680 0.533960
97 0.313578 0.076204 0.610218
98 0.096412 0.388955 0.514633
99 0.128096 0.219235 0.652669
100 0.352594 0.322882 0.324524
101 0.104648 0.057263 0.838089
102 0.302008 0.395548 0.302444
103 0.151431 0.436842 0.411726
104 0.139075 0.660561 0.200364
105 0.107779 0.856988 0.035233
106 0.365959 0.349271 0.284770
107 0.212292 0.631549 0.156159
108 0.424784 0.136636 0.438580
109 0.721633 0.080231 0.198136
110 0.021620 0.059024 0.919356
111 0.140476 0.438159 0.421365
112 0.632002 0.254618 0.113380
113 0.047913 0.844380 0.107707
114 0.174634 0.292413 0.532953
115 0.100894 0.120093 0.779013
116 0.334436 0.548705 0.116859
117 0.102102 0.846243 0.051655
118 0.156495 0.158297 0.685208
119 0.129631 0.310234 0.560135
120 0.278274 0.435811 0.285915
121 0.087736 0.105743 0.806521
122 0.743557 0.029594 0.226848
123 0.297640 0.413088 0.289271
124 0.580617 0.115469 0.303914
125 0.022530 0.478587 0.498883
126 0.025032 0.576158 0.398810
127 0.302488 0.179321 0.518191
128 0.160016 0.587391 0.252593
129 0.285020 0.428606 0.286374
130 0.304977 0.449599 0.245423
131 0.105340 0.248095 0.646565
132 0.123845 0.853532 0.022623
133 0.428693 0.516511 0.054796
134 0.169013 0.637962 0.193025
135 0.502524 0.304055 0.193421
136 0.427776 0.445790 0.126434
137 0.413089 0.146011 0.440901
138 0.038761 0.625258 0.335981
139 0.342346 0.515809 0.141845
140 0.108328 0.572061 0.319611
141 0.595584 0.002004 0.402411
142 0.691069 0.203494 0.105437
143 0.188119 0.659323 0.152557
144 0.137058 0.839973 0.022969
145 0.011064 0.311119 0.677817
146 0.162586 0.287187 0.550227
147 0.002245 0.377887 0.619867
148 0.261884 0.123569 0.614547
149 0.572904 0.010344 0.416753
150 0.136353 0.563149 0.300498
Hitung centroid berdasarkan matriks keanggotaan U#
def calculate_centroids(X, U, m):
um = U ** m
centroids = (um.T @ X) / np.sum(um.T, axis=1)[:, None]
return centroids
centroids = calculate_centroids(X, U, m)
print("=== Centroid Awal (Iterasi ke-1) ===")
for i, centroid in enumerate(centroids):
print(f"Centroid Cluster {i+1}: {centroid}")
=== Centroid Awal (Iterasi ke-1) ===
Centroid Cluster 1: [5.67099986 3.09161079 3.33060669 1.00382155]
Centroid Cluster 2: [5.99847964 3.04358399 4.14145251 1.35344364]
Centroid Cluster 3: [5.89566621 3.13620694 3.79120818 1.26212358]
Update matriks keanggotaan U#
def update_membership(X, centroids, m):
n = X.shape[0]
c = centroids.shape[0]
U_new = np.zeros((n, c))
for i in range(n):
distances = np.linalg.norm(X[i] - centroids, axis=1)
for j in range(c):
denom = np.sum((distances[j] / distances) ** (2 / (m - 1)))
U_new[i, j] = 1 / denom
return U_new
# Perbarui keanggotaan
U_new = update_membership(X, centroids, m)
# Buat DataFrame dan atur urutan kolom (id di paling kiri)
df_U_new = pd.DataFrame(U_new, columns=[f"Cluster_{i+1}" for i in range(k)])
df_U_new.insert(0, "id", df_U_new.index + 1) # Tambahkan ID di kolom pertama
# Cetak hasil
print("=== Matriks Keanggotaan Baru (Setelah Iterasi ke-1) ===")
print(df_U_new.to_string(index=False))
=== Matriks Keanggotaan Baru (Setelah Iterasi ke-1) ===
id Cluster_1 Cluster_2 Cluster_3
1 0.468872 0.231365 0.299763
2 0.469846 0.232536 0.297618
3 0.461289 0.237562 0.301150
4 0.467397 0.234201 0.298401
5 0.465794 0.233163 0.301044
6 0.475765 0.224122 0.300113
7 0.462635 0.236100 0.301265
8 0.474331 0.228452 0.297217
9 0.457272 0.241233 0.301495
10 0.472748 0.230726 0.296526
11 0.469937 0.229412 0.300651
12 0.475078 0.228318 0.296603
13 0.466093 0.235203 0.298704
14 0.444714 0.249166 0.306120
15 0.444017 0.244706 0.311277
16 0.441564 0.244212 0.314224
17 0.457026 0.236571 0.306404
18 0.470465 0.230108 0.299426
19 0.474855 0.224595 0.300550
20 0.467595 0.230889 0.301516
21 0.489268 0.218548 0.292184
22 0.471945 0.228196 0.299859
23 0.444866 0.247250 0.307884
24 0.495372 0.215007 0.289621
25 0.489840 0.219404 0.290756
26 0.482195 0.224946 0.292860
27 0.483461 0.222313 0.294226
28 0.474782 0.227488 0.297730
29 0.471275 0.229999 0.298726
30 0.474403 0.229499 0.296098
31 0.477619 0.227702 0.294680
32 0.480830 0.223098 0.296072
33 0.454636 0.238603 0.306761
34 0.448011 0.241839 0.310149
35 0.474957 0.229144 0.295898
36 0.461632 0.236924 0.301444
37 0.464054 0.233673 0.302273
38 0.462699 0.235520 0.301782
39 0.454302 0.242824 0.302874
40 0.475713 0.227428 0.296859
41 0.464455 0.234075 0.301470
42 0.448665 0.247760 0.303576
43 0.454171 0.242425 0.303404
44 0.483091 0.221541 0.295368
45 0.489360 0.216760 0.293880
46 0.469392 0.232730 0.297878
47 0.470468 0.229311 0.300222
48 0.463040 0.236612 0.300348
49 0.470091 0.229533 0.300376
50 0.470516 0.231112 0.298373
51 0.175998 0.499819 0.324183
52 0.099371 0.638418 0.262211
53 0.171685 0.512784 0.315531
54 0.265346 0.383629 0.351025
55 0.124092 0.601438 0.274470
56 0.112875 0.621611 0.265514
57 0.118984 0.599998 0.281018
58 0.495037 0.216613 0.288350
59 0.133050 0.580584 0.286366
60 0.306379 0.321501 0.372121
61 0.420063 0.267594 0.312344
62 0.028983 0.843865 0.127152
63 0.254495 0.401489 0.344016
64 0.100811 0.658200 0.240989
65 0.393700 0.167316 0.438984
66 0.134150 0.560885 0.304965
67 0.115160 0.603044 0.281796
68 0.173055 0.464172 0.362773
69 0.174245 0.519190 0.306565
70 0.286370 0.341827 0.371804
71 0.134025 0.573893 0.292082
72 0.072838 0.633763 0.293400
73 0.156818 0.550998 0.292183
74 0.116217 0.626122 0.257661
75 0.087709 0.666963 0.245329
76 0.118750 0.596024 0.285227
77 0.163953 0.529748 0.306299
78 0.164409 0.527911 0.307680
79 0.070841 0.730034 0.199126
80 0.527498 0.174005 0.298497
81 0.345927 0.302308 0.351765
82 0.402269 0.263693 0.334039
83 0.175365 0.390391 0.434244
84 0.159690 0.545238 0.295072
85 0.156656 0.520691 0.322653
86 0.101503 0.617989 0.280509
87 0.144612 0.554938 0.300450
88 0.167127 0.527850 0.305023
89 0.116109 0.486976 0.396915
90 0.242514 0.391498 0.365988
91 0.182224 0.494312 0.323464
92 0.080634 0.703808 0.215558
93 0.171595 0.456967 0.371438
94 0.488437 0.220936 0.290627
95 0.147398 0.521643 0.330960
96 0.088188 0.600740 0.311072
97 0.083671 0.635607 0.280722
98 0.051674 0.778405 0.169921
99 0.558083 0.179542 0.262375
100 0.110018 0.550507 0.339475
101 0.223446 0.444731 0.331823
102 0.173787 0.518699 0.307514
103 0.221515 0.448661 0.329823
104 0.192534 0.490861 0.316605
105 0.209973 0.464113 0.325914
106 0.246295 0.419599 0.334106
107 0.254113 0.405901 0.339986
108 0.234904 0.433891 0.331205
109 0.213124 0.464167 0.322709
110 0.236096 0.427629 0.336275
111 0.171655 0.513219 0.315126
112 0.181477 0.507174 0.311349
113 0.201101 0.474545 0.324355
114 0.186253 0.499601 0.314145
115 0.195768 0.480125 0.324107
116 0.192063 0.483490 0.324447
117 0.188471 0.494924 0.316604
118 0.252738 0.409894 0.337367
119 0.254203 0.411617 0.334180
120 0.188184 0.503832 0.307984
121 0.214783 0.454945 0.330272
122 0.174760 0.511412 0.313828
123 0.249657 0.416495 0.333848
124 0.150305 0.557038 0.292657
125 0.207837 0.464303 0.327860
126 0.224995 0.444091 0.330914
127 0.135215 0.582498 0.282287
128 0.137691 0.575481 0.286828
129 0.199854 0.479348 0.320797
130 0.218996 0.452670 0.328334
131 0.232651 0.436238 0.331111
132 0.251164 0.410984 0.337852
133 0.202371 0.475290 0.322339
134 0.155696 0.550753 0.293551
135 0.198525 0.487080 0.314395
136 0.240498 0.424787 0.334715
137 0.208877 0.460798 0.330325
138 0.186842 0.496536 0.316622
139 0.128877 0.590531 0.280592
140 0.200330 0.473827 0.325843
141 0.210137 0.461108 0.328755
142 0.197380 0.474286 0.328334
143 0.173787 0.518699 0.307514
144 0.219151 0.450426 0.330423
145 0.216797 0.451322 0.331882
146 0.193764 0.481757 0.324480
147 0.171583 0.523069 0.305348
148 0.176326 0.509957 0.313717
149 0.198043 0.474054 0.327903
150 0.159262 0.539248 0.301490
Hitung Fungsi Objektif dan Cek Konvergensi#
# Fungsi objektif
def objective_function(X, U, centroids, m):
n = X.shape[0]
c = centroids.shape[0]
J = 0
for i in range(n):
for j in range(c):
dist = np.linalg.norm(X[i] - centroids[j])
J += (U[i, j] ** m) * (dist ** 2)
return J
J = objective_function(X, U_new, centroids, m)
print(f"=== Fungsi Objektif (J) Iterasi ke-1 ===\nJ = {J:.4f}")
# Cek konvergensi
epsilon = 0.01
delta = np.linalg.norm(U_new - U)
print(f"\nPerubahan matriks keanggotaan (delta) = {delta:.6f}")
if delta < epsilon:
print("โ
Matriks keanggotaan sudah konvergen (berhenti iterasi).")
else:
print("โ Belum konvergen, lanjut ke iterasi berikutnya.")
# Lakukan PCA untuk mereduksi fitur dari 4 ke 2 dimensi
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
# Tentukan cluster dengan keanggotaan tertinggi tiap data (hard clustering)
cluster_labels = np.argmax(U_new, axis=1)
# Plot data hasil PCA, warna berdasarkan cluster
plt.figure(figsize=(10, 7))
colors = ['red', 'green', 'blue']
for i in range(k):
cluster_points = X_pca[cluster_labels == i]
plt.scatter(cluster_points[:, 0], cluster_points[:, 1],
label=f'Cluster {i+1}', alpha=0.6, s=50, color=colors[i])
plt.title("Hasil Clustering FCM Iris Dataset (Visualisasi PCA)")
plt.xlabel("PCA 1")
plt.ylabel("PCA 2")
plt.legend()
plt.grid(True)
plt.show()
=== Fungsi Objektif (J) Iterasi ke-1 ===
J = 211.9498
Perubahan matriks keanggotaan (delta) = 5.190565
โ Belum konvergen, lanjut ke iterasi berikutnya.
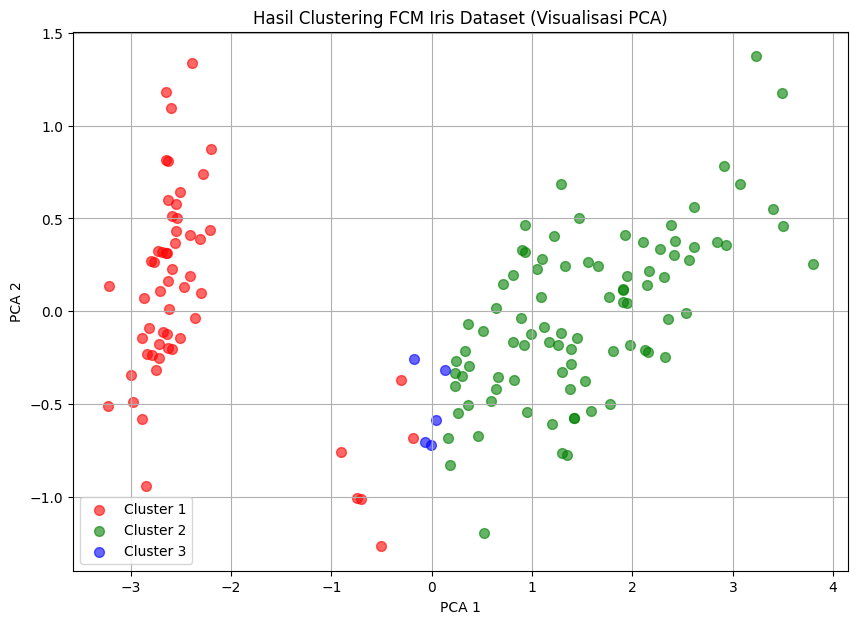
Karena dari perhitungan diatas belum mencapai konvergensi maka Akan dilakukan perhitungan ulang pada iterasi hingga mencapai konvergensi
# === Fungsi bantu ===
def euclidean_distance(a, b):
return np.linalg.norm(a - b, axis=1)
def calculate_centroids(X, U, m):
um = U ** m
centroids = (um.T @ X) / np.sum(um.T, axis=1)[:, None]
return centroids
def update_membership(X, centroids, m):
n = X.shape[0]
c = centroids.shape[0]
U_new = np.zeros((n, c))
for i in range(n):
distances = np.linalg.norm(X[i] - centroids, axis=1)
for j in range(c):
denom = np.sum((distances[j] / distances) ** (2 / (m - 1)))
U_new[i, j] = 1 / denom
return U_new
def objective_function(X, U, centroids, m):
n = X.shape[0]
c = centroids.shape[0]
J = 0
for i in range(n):
for j in range(c):
dist = np.linalg.norm(X[i] - centroids[j])
J += (U[i, j] ** m) * (dist ** 2)
return J
# === Load data Iris ===
iris = load_iris()
X = iris.data
n, d = X.shape
k = 3
m = 2
epsilon = 0.01
max_iter = 100
np.random.seed(42)
# Inisialisasi keanggotaan acak (dengan baris = data, kolom = cluster)
U = np.random.dirichlet(np.ones(k), size=n)
# === Iterasi ===
for iteration in range(1, max_iter + 1):
print(f"\n====== ITERASI KE-{iteration} ======")
# Hitung centroid
centroids = calculate_centroids(X, U, m)
print("\n๐ Centroid:")
for idx, c in enumerate(centroids):
print(f"Cluster {idx+1}: {c}")
# Update keanggotaan
U_new = update_membership(X, centroids, m)
print("\n๐ Matriks Keanggotaan (5 data pertama):")
df_U_new = pd.DataFrame(U_new, columns=[f"C{i+1}" for i in range(k)])
print(df_U_new.head().to_string(index=False))
# Hitung fungsi objektif
J = objective_function(X, U_new, centroids, m)
print(f"\n๐ Fungsi Objektif (J): {J:.6f}")
# Cek konvergensi
delta = np.linalg.norm(U_new - U)
print(f"๐ Perubahan keanggotaan (delta): {delta:.6f}")
if delta < epsilon:
print("\nโ
Konvergensi tercapai. Iterasi dihentikan.")
break
U = U_new # simpan untuk iterasi berikutnya
# === Hasil akhir ===
print("\n======== HASIL AKHIR ========")
print("๐ Centroid akhir:")
for idx, c in enumerate(centroids):
print(f"Cluster {idx+1}: {c}")
print("\n๐ Keanggotaan akhir (5 data pertama):")
print(df_U_new.head().to_string(index=False))
print(f"\n๐ Fungsi Objektif akhir: {J:.6f}")
====== ITERASI KE-1 ======
๐ Centroid:
Cluster 1: [6.06673919 3.00422155 4.16771426 1.37476747]
Cluster 2: [5.85048499 3.06034261 3.8023977 1.20959388]
Cluster 3: [5.63287974 3.1153372 3.26640646 0.99226272]
๐ Matriks Keanggotaan (5 data pertama):
C1 C2 C3
0.217205 0.294142 0.488653
0.218217 0.294863 0.486920
0.223350 0.298084 0.478566
0.219065 0.296063 0.484872
0.218886 0.295383 0.485731
๐ Fungsi Objektif (J): 207.462652
๐ Perubahan keanggotaan (delta): 5.720933
====== ITERASI KE-2 ======
๐ Centroid:
Cluster 1: [6.21068093 2.95698086 4.64895615 1.56593278]
Cluster 2: [5.82662119 3.00516876 3.82861947 1.22327775]
Cluster 3: [5.2690505 3.25460263 2.26381149 0.58115577]
๐ Matriks Keanggotaan (5 data pertama):
C1 C2 C3
0.058691 0.106079 0.835230
0.063467 0.115005 0.821528
0.072616 0.128017 0.799367
0.067576 0.121863 0.810561
0.062521 0.112008 0.825470
๐ Fungsi Objektif (J): 123.393639
๐ Perubahan keanggotaan (delta): 4.076931
====== ITERASI KE-3 ======
๐ Centroid:
Cluster 1: [6.4044565 2.94065361 5.0882252 1.76980103]
Cluster 2: [5.80453386 2.76582206 4.15657737 1.32046313]
Cluster 3: [5.03232543 3.40524751 1.54991165 0.28092839]
๐ Matriks Keanggotaan (5 data pertama):
C1 C2 C3
0.002339 0.004277 0.993384
0.011126 0.020972 0.967902
0.010854 0.019842 0.969304
0.014861 0.028021 0.957118
0.003643 0.006600 0.989757
๐ Fungsi Objektif (J): 70.083851
๐ Perubahan keanggotaan (delta): 3.008571
====== ITERASI KE-4 ======
๐ Centroid:
Cluster 1: [6.55236452 2.97690628 5.33906123 1.90803185]
Cluster 2: [5.78729852 2.72566773 4.21548198 1.32272435]
Cluster 3: [5.00690117 3.41749027 1.48277921 0.25307865]
๐ Matriks Keanggotaan (5 data pertama):
C1 C2 C3
0.001204 0.002442 0.996354
0.008975 0.018900 0.972125
0.007643 0.015544 0.976812
0.012073 0.025468 0.962459
0.002014 0.004045 0.993940
๐ Fungsi Objektif (J): 63.341534
๐ Perubahan keanggotaan (delta): 1.333176
====== ITERASI KE-5 ======
๐ Centroid:
Cluster 1: [6.64111276 3.00846771 5.46886063 1.97457743]
Cluster 2: [5.80342973 2.729585 4.24136474 1.33430962]
Cluster 3: [5.0044585 3.41713018 1.47900781 0.25169828]
๐ Matriks Keanggotaan (5 data pertama):
C1 C2 C3
0.001112 0.002376 0.996512
0.008297 0.018406 0.973297
0.007016 0.015005 0.977979
0.011166 0.024805 0.964029
0.001852 0.003914 0.994233
๐ Fungsi Objektif (J): 61.552810
๐ Perubahan keanggotaan (delta): 0.728302
====== ITERASI KE-6 ======
๐ Centroid:
Cluster 1: [6.69145304 3.02591396 5.53794674 2.00708894]
Cluster 2: [5.82621666 2.73774917 4.27374176 1.3512859 ]
Cluster 3: [5.00407403 3.416547 1.47922351 0.25187142]
๐ Matriks Keanggotaan (5 data pertama):
C1 C2 C3
0.001082 0.002343 0.996575
0.007980 0.017916 0.974105
0.006758 0.014629 0.978613
0.010743 0.024150 0.965107
0.001798 0.003851 0.994351
๐ Fungsi Objektif (J): 60.946776
๐ Perubahan keanggotaan (delta): 0.455904
====== ITERASI KE-7 ======
๐ Centroid:
Cluster 1: [6.7214824 3.0358165 5.57785699 2.02486587]
Cluster 2: [5.84578167 2.7450818 4.30176907 1.36563446]
Cluster 3: [5.00398004 3.41592531 1.48001314 0.25226072]
๐ Matriks Keanggotaan (5 data pertama):
C1 C2 C3
0.001072 0.002323 0.996605
0.007802 0.017512 0.974686
0.006623 0.014342 0.979035
0.010508 0.023612 0.965880
0.001778 0.003812 0.994410
๐ Fungsi Objektif (J): 60.696999
๐ Perubahan keanggotaan (delta): 0.299058
====== ITERASI KE-8 ======
๐ Centroid:
Cluster 1: [6.74031052 3.04182176 5.60247394 2.03546672]
Cluster 2: [5.86016356 2.75048671 4.32240595 1.37611523]
Cluster 3: [5.00395152 3.41538228 1.4807971 0.25262869]
๐ Matriks Keanggotaan (5 data pertama):
C1 C2 C3
0.001070 0.002314 0.996617
0.007693 0.017221 0.975086
0.006546 0.014141 0.979313
0.010364 0.023225 0.966411
0.001771 0.003791 0.994439
๐ Fungsi Objektif (J): 60.588230
๐ Perubahan keanggotaan (delta): 0.197184
====== ITERASI KE-9 ======
๐ Centroid:
Cluster 1: [6.75243931 3.0456001 5.61815325 2.04204576]
Cluster 2: [5.87005644 2.75417086 4.33662498 1.38333869]
Cluster 3: [5.00394537 3.41496777 1.48142375 0.25291695]
๐ Matriks Keanggotaan (5 data pertama):
C1 C2 C3
0.001070 0.002309 0.996621
0.007624 0.017023 0.975353
0.006498 0.014007 0.979495
0.010273 0.022962 0.966766
0.001768 0.003779 0.994453
๐ Fungsi Objektif (J): 60.540943
๐ Perubahan keanggotaan (delta): 0.129411
====== ITERASI KE-10 ======
๐ Centroid:
Cluster 1: [6.76033358 3.04801445 5.62826291 2.04619632]
Cluster 2: [5.87664902 2.75660176 4.34612668 1.3881789 ]
Cluster 3: [5.00394739 3.4146737 1.48188019 0.25312471]
๐ Matriks Keanggotaan (5 data pertama):
C1 C2 C3
0.001070 0.002307 0.996623
0.007579 0.016892 0.975529
0.006468 0.013919 0.979613
0.010214 0.022788 0.966998
0.001768 0.003772 0.994460
๐ Fungsi Objektif (J): 60.520626
๐ Perubahan keanggotaan (delta): 0.084487
====== ITERASI KE-11 ======
๐ Centroid:
Cluster 1: [6.76548172 3.04956641 5.63480513 2.04883518]
Cluster 2: [5.88097306 2.75818394 4.35237834 1.39137306]
Cluster 3: [5.0039516 3.41447326 1.48219666 0.25326791]
๐ Matriks Keanggotaan (5 data pertama):
C1 C2 C3
0.001071 0.002306 0.996624
0.007550 0.016807 0.975643
0.006449 0.013863 0.979689
0.010176 0.022674 0.967150
0.001768 0.003768 0.994464
๐ Fungsi Objektif (J): 60.511987
๐ Perubahan keanggotaan (delta): 0.054935
====== ITERASI KE-12 ======
๐ Centroid:
Cluster 1: [6.76883455 3.05056625 5.63904059 2.05052061]
Cluster 2: [5.88378628 2.75920782 4.35645734 1.39346244]
Cluster 3: [5.00395565 3.41433966 1.48240996 0.25336409]
๐ Matriks Keanggotaan (5 data pertama):
C1 C2 C3
0.001071 0.002305 0.996624
0.007532 0.016751 0.975717
0.006437 0.013826 0.979737
0.010152 0.022600 0.967248
0.001768 0.003766 0.994467
๐ Fungsi Objektif (J): 60.508341
๐ Perubahan keanggotaan (delta): 0.035620
====== ITERASI KE-13 ======
๐ Centroid:
Cluster 1: [6.77101343 3.05121092 5.64178106 2.05160042]
Cluster 2: [5.88560897 2.75986885 4.35910626 1.39482194]
Cluster 3: [5.00395886 3.41425177 1.48255131 0.25342769]
๐ Matriks Keanggotaan (5 data pertama):
C1 C2 C3
0.001071 0.002305 0.996624
0.007520 0.016715 0.975765
0.006429 0.013802 0.979769
0.010136 0.022552 0.967312
0.001768 0.003764 0.994468
๐ Fungsi Objektif (J): 60.506810
๐ Perubahan keanggotaan (delta): 0.023054
====== ITERASI KE-14 ======
๐ Centroid:
Cluster 1: [6.77242648 3.05162671 5.64355286 2.05229373]
Cluster 2: [5.88678736 2.76029522 4.36082181 1.39570365]
Cluster 3: [5.00396119 3.4141944 1.48264404 0.25346936]
๐ Matriks Keanggotaan (5 data pertama):
C1 C2 C3
0.001072 0.002305 0.996624
0.007512 0.016692 0.975796
0.006424 0.013787 0.979789
0.010126 0.022521 0.967353
0.001768 0.003763 0.994469
๐ Fungsi Objektif (J): 60.506170
๐ Perubahan keanggotaan (delta): 0.014903
====== ITERASI KE-15 ======
๐ Centroid:
Cluster 1: [6.77334139 3.05189491 5.64469762 2.05273954]
Cluster 2: [5.88754836 2.76057016 4.3619311 1.39627433]
Cluster 3: [5.0039628 3.41415712 1.48270448 0.2534965 ]
๐ Matriks Keanggotaan (5 data pertama):
C1 C2 C3
0.001072 0.002305 0.996624
0.007507 0.016677 0.975816
0.006420 0.013777 0.979802
0.010119 0.022501 0.967379
0.001768 0.003763 0.994469
๐ Fungsi Objektif (J): 60.505902
๐ Perubahan keanggotaan (delta): 0.009626
โ
Konvergensi tercapai. Iterasi dihentikan.
======== HASIL AKHIR ========
๐ Centroid akhir:
Cluster 1: [6.77334139 3.05189491 5.64469762 2.05273954]
Cluster 2: [5.88754836 2.76057016 4.3619311 1.39627433]
Cluster 3: [5.0039628 3.41415712 1.48270448 0.2534965 ]
๐ Keanggotaan akhir (5 data pertama):
C1 C2 C3
0.001072 0.002305 0.996624
0.007507 0.016677 0.975816
0.006420 0.013777 0.979802
0.010119 0.022501 0.967379
0.001768 0.003763 0.994469
๐ Fungsi Objektif akhir: 60.505902
# Reduksi dimensi data asli ke 2D menggunakan PCA
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
# Tentukan label cluster berdasarkan nilai keanggotaan maksimum
labels = np.argmax(U, axis=1)
# Transformasi centroid ke ruang PCA
centroids_pca = pca.transform(centroids)
# Plot data dengan warna berdasarkan cluster
plt.figure(figsize=(8, 6))
colors = ['red', 'green', 'blue']
for i in range(k):
plt.scatter(X_pca[labels == i, 0], X_pca[labels == i, 1],
color=colors[i], alpha=0.6, label=f'Cluster {i+1}')
# Plot centroid
plt.scatter(centroids_pca[:, 0], centroids_pca[:, 1],
color='black', marker='X', s=200, label='Centroids')
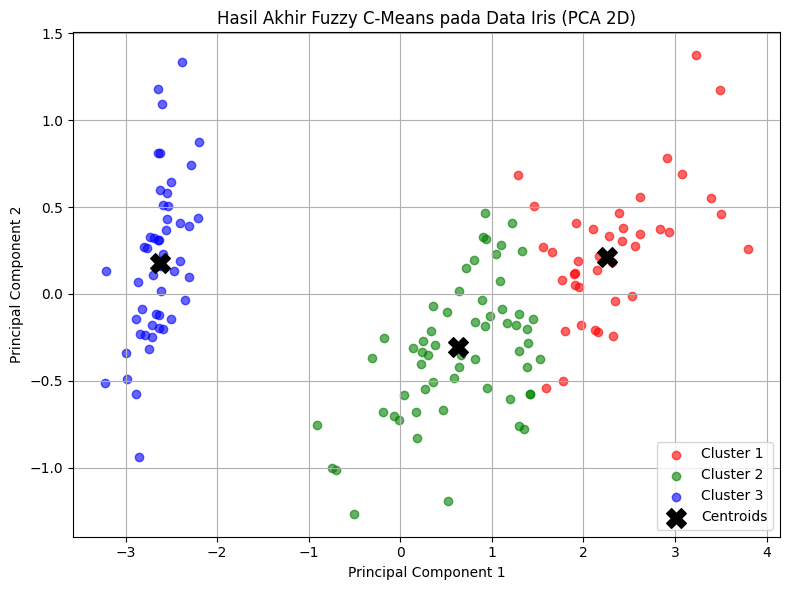
plt.title('Hasil Akhir Fuzzy C-Means pada Data Iris (PCA 2D)')
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
