Local Outlier Factor (LOF)#
Apa Itu LOF?#
Local Outlier Factor (LOF) adalah metode deteksi outlier berbasis kepadatan (density-based).
LOF membandingkan kepadatan lokal suatu titik dengan tetangga terdekatnya.
Jika suatu titik memiliki kepadatan jauh lebih rendah dibandingkan tetangganya, maka titik tersebut adalah outlier.
Tahapan Perhitungan LOF#
Proses deteksi outlier dengan Local Outlier Factor (LOF) terdiri dari beberapa langkah:
1️. Tentukan K (Jumlah Tetangga Terdekat)#
Pilih jumlah tetangga K (misalnya K = 2 atau 3).
Setiap titik akan dibandingkan dengan K tetangga terdekatnya.
2️. Hitung Jarak Tetangga Terdekat (k-distance)#
Gunakan jarak Euclidean untuk menghitung seberapa jauh suatu titik dari tetangga terdekatnya:
\[ d(p, q) = \sqrt{(x_p - x_q)^2 + (y_p - y_q)^2} \]Tentukan k-distance(p), yaitu jarak antara titik p dan tetangga ke-K.
3️. Hitung Reachability Distance#
Jarak dapat dijangkau (reachability distance) antara p dan q dihitung sebagai:
\[ \text{reach-dist}_k(p, q) = \max(k\text{-distance}(q), d(p, q)) \]Jika jarak antar titik lebih kecil dari k-distance, gunakan k-distance.
4️. Hitung Kepadatan Lokal (Local Reachability Density - LRD)#
Kepadatan lokal dari suatu titik p dihitung dengan:
\[ LRD_k(p) = \frac{k}{\sum_{q \in N_k(p)} \text{reach-dist}_k(p, q)} \]Semakin kecil LRD, semakin besar kemungkinan titik itu adalah outlier.
5️ Hitung Local Outlier Factor (LOF)#
Nilai LOF suatu titik p didefinisikan sebagai rasio rata-rata kepadatan tetangga terhadap kepadatan titik itu sendiri:
\[ LOF_k(p) = \frac{\sum_{q \in N_k(p)} \frac{LRD_k(q)}{LRD_k(p)}}{|N_k(p)|} \]Jika ( LOF_k(p) > 1.5 ), maka titik tersebut adalah outlier.
📊 Contoh Perhitungan Manual LOF (10 Baris, 2 Kolom)#
Misalkan kita punya dataset koordinat berikut:
ID |
X |
Y |
|---|---|---|
A |
2 |
3 |
B |
3 |
4 |
C |
4 |
2 |
D |
5 |
5 |
E |
3 |
3 |
F |
4 |
4 |
G |
6 |
2 |
H |
5 |
3 |
I |
7 |
4 |
J |
100 |
100 |
🔢 Langkah Perhitungan LOF untuk Titik J#
1️. Tentukan K = 2 Tetangga Terdekat
Tetangga terdekat J adalah I (7,4) dan H (5,3)
Hitung k-distance(J) → Jarak Euclidean dari J ke I & H
- \[ d(J, I) = \sqrt{(100-7)^2 + (100-4)^2} = 131.82 \]
- \[ d(J, H) = \sqrt{(100-5)^2 + (100-3)^2} = 134.35 \]
2️. Hitung Reachability Distance
- \[ \text{reach-dist}(J, I) = \max(k\text{-distance}(I), d(J, I)) = 131.82 \]
- \[ \text{reach-dist}(J, H) = \max(k\text{-distance}(H), d(J, H)) = 134.35 \]
3️. Hitung Local Reachability Density (LRD)
- \[ LRD_J = \frac{2}{131.82 + 134.35} = 0.00752 \]
4️. Hitung Local Outlier Factor (LOF)
- \[ LOF_J = \frac{(LRD_I / LRD_J) + (LRD_H / LRD_J)}{2} \]
Jika hasil LOF > 1.5, maka J adalah outlier ✅
Kesimpulan#
Berdasarkan hasil perhitungan LOF, titik J (100,100) memiliki nilai LOF tinggi.
Artinya, titik ini berada jauh dari kepadatan lokal dan dapat dianggap sebagai outlier.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.neighbors import LocalOutlierFactor
# Data dengan ID
ids = ["A", "B", "C", "D", "E", "F", "G", "H", "I", "J"]
# Data points (X, Y)
data = np.array([
[2, 3], [3, 4], [4, 2], [5, 5], [3, 3],
[4, 4], [6, 2], [5, 3], [7, 4], [100, 100]
])
# Apply Local Outlier Factor (LOF)
lof = LocalOutlierFactor(n_neighbors=2)
outlier_scores = lof.fit_predict(data)
# Identify outliers (-1 indicates outliers)
outliers = np.where(outlier_scores == -1)[0]
# Mendapatkan LOF scores dan Local Reachability Density (LRD)
lof_scores = lof.negative_outlier_factor_ # Semakin kecil, semakin outlier
lrd_scores = 1 / np.abs(lof_scores) # LRD adalah kebalikan dari LOF
# Menandai outlier (Yes jika outlier, No jika bukan)
outlier_flags = ["Yes" if i in outliers else "No" for i in range(len(data))]
# Membuat DataFrame
df = pd.DataFrame(data, columns=["X", "Y"])
df.insert(0, "ID", ids)
df["Outlier"] = outlier_flags
df["LOF Score"] = lof_scores
df["LRD Score"] = lrd_scores
# Menampilkan DataFrame
print(df)
# Plot data
outlier_points = data[outliers]
plt.scatter(data[:, 0], data[:, 1], label="Data Points", color='blue')
plt.scatter(outlier_points[:, 0], outlier_points[:, 1], label="Outliers", color='red', marker='x', s=100)
# Labels and legend
plt.xlabel("X")
plt.ylabel("Y")
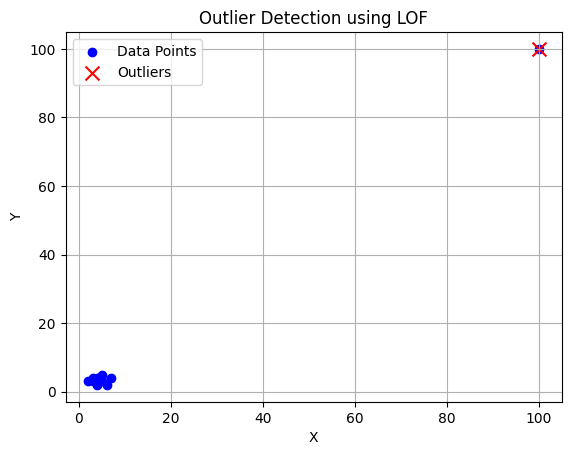
plt.title("Outlier Detection using LOF")
plt.legend()
plt.grid()
plt.show()
ID X Y Outlier LOF Score LRD Score
0 A 2 3 No -1.000000 1.000000
1 B 3 4 No -0.902369 1.108194
2 C 4 2 No -1.085786 0.920991
3 D 5 5 No -1.172589 0.852814
4 E 3 3 No -1.000000 1.000000
5 F 4 4 No -1.060660 0.942809
6 G 6 2 No -1.207107 0.828427
7 H 5 3 No -0.971405 1.029437
8 I 7 4 No -1.309858 0.763441
9 J 100 100 Yes -69.213663 0.014448
Penjelasan Code#
Membutuhkan library berikut:
numpy digunakan untuk operasi numerik dan manipulasi array.
pandas digunakan untuk menyimpan dan memproses data dalam bentuk tabel (DataFrame).
matplotlib.pyplot digunakan untuk visualisasi data dalam bentuk scatter plot.
LocalOutlierFactor dari sklearn.neighbors adalah metode yang digunakan untuk mendeteksi outlier dalam dataset.
Tampung data pada variabel ids atau jika anda menggunakan database, anda bisa menggunakan aiven dan dbeaver lalu masukkan informasi database dan connect.
Buat variabel untuk menentukan nilai k seperti di kode yaitu 2 Melakukan training pada dataset dan mengembalikan prediksi (-1 untuk outlier, 1 untuk inlier/non-outlier).
np.where(outlier_scores == -1)[0] akan mengembalikan indeks dari data yang diklasifikasikan sebagai outlier oleh LOF.
Nilai yang lebih kecil menunjukkan bahwa titik lebih jauh dari tetangganya dan lebih mungkin menjadi outlier.
Local Reachability Density (LRD) adalah kebalikan dari LOF score.
LRD menunjukkan kepadatan relatif dari sebuah titik dibandingkan dengan titik di sekitarnya.
Yes untuk outlier dan no bukan
Kemudian tampilkan dataframe
–
data[:, 0] dan data[:, 1] digunakan untuk mendapatkan semua nilai X dan Y untuk scatter plot.
Titik data normal diberi warna biru.
Outlier diberi warna merah dan berbentuk “X”.
