K-Means Clustering#
Pengertian K-Means Clustering#
K-Means Clustering adalah teknik pengelompokan data yang memisahkan data ke dalam cluster, mengelompokkan data dengan fitur yang sama bersama-sama dan mengelompokkan data dengan karakteristik yang berbeda ke dalam kelompok yang berbeda dengan centroid sebagai acuannya. Metode k-means membagi data menjadi beberapa kelompok sehingga data dengan karakteristik yang sama berada pada cluster yang sama dan data dengan karakteristik yang berbeda berada pada cluster yang berbeda
Manfaat Clustering#
Clustering merupakan metode segmentasi data yang sangat berguna dalam prediksi dan analisa masalah bisnis tertentu. Misalnya Segmentasi pasar, marketing dan pemetaan zonasi wilayah.
Identifikasi obyek dalam bidang berbagai bidang seperti computer vision dan image processing.
Hasil clustering yang baik akan menghasilkan tingkat kesamaan yang tinggi dalam satu kelas dan tingkat kesamaan yang rendah antar kelas. Kesamaan yang dimaksud merupakan pengukuran secara numerik terhadap dua buah objek. Nilai kesamaan antar kedua objek akan semakin tinggi jika kedua objek yang dibandingkan memiliki kemiripan yang tinggi. Begitu juga dengan sebaliknya. Kualitas hasil clustering sangat bergantung pada metode yang dipakai
Instalasi Library#
!pip install pymysql
!pip install pandas
!pip install psycopg2-binary
!pip install sqlalchemy
!pip install python-dotenv
Requirement already satisfied: pymysql in /usr/local/python/3.12.1/lib/python3.12/site-packages (1.1.1)
[notice] A new release of pip is available: 24.3.1 -> 25.1.1
[notice] To update, run: python3 -m pip install --upgrade pip
Requirement already satisfied: pandas in /home/codespace/.local/lib/python3.12/site-packages (2.2.3)
Requirement already satisfied: numpy>=1.26.0 in /home/codespace/.local/lib/python3.12/site-packages (from pandas) (2.2.0)
Requirement already satisfied: python-dateutil>=2.8.2 in /home/codespace/.local/lib/python3.12/site-packages (from pandas) (2.9.0.post0)
Requirement already satisfied: pytz>=2020.1 in /home/codespace/.local/lib/python3.12/site-packages (from pandas) (2024.2)
Requirement already satisfied: tzdata>=2022.7 in /home/codespace/.local/lib/python3.12/site-packages (from pandas) (2024.2)
Requirement already satisfied: six>=1.5 in /home/codespace/.local/lib/python3.12/site-packages (from python-dateutil>=2.8.2->pandas) (1.17.0)
[notice] A new release of pip is available: 24.3.1 -> 25.1.1
[notice] To update, run: python3 -m pip install --upgrade pip
Requirement already satisfied: psycopg2-binary in /usr/local/python/3.12.1/lib/python3.12/site-packages (2.9.10)
[notice] A new release of pip is available: 24.3.1 -> 25.1.1
[notice] To update, run: python3 -m pip install --upgrade pip
Requirement already satisfied: sqlalchemy in /usr/local/python/3.12.1/lib/python3.12/site-packages (2.0.38)
Requirement already satisfied: greenlet!=0.4.17 in /usr/local/python/3.12.1/lib/python3.12/site-packages (from sqlalchemy) (3.1.1)
Requirement already satisfied: typing-extensions>=4.6.0 in /home/codespace/.local/lib/python3.12/site-packages (from sqlalchemy) (4.12.2)
[notice] A new release of pip is available: 24.3.1 -> 25.1.1
[notice] To update, run: python3 -m pip install --upgrade pip
Requirement already satisfied: python-dotenv in /usr/local/python/3.12.1/lib/python3.12/site-packages (1.0.1)
[notice] A new release of pip is available: 24.3.1 -> 25.1.1
[notice] To update, run: python3 -m pip install --upgrade pip
import psycopg2
import pymysql
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
from sklearn.metrics import silhouette_score
from sklearn.cluster import KMeans
from mpl_toolkits.mplot3d import Axes3D
Persiapan Data#
Masukkan informasi database dari aiven seperti code dibawah ini
def get_pg_data():
conn = psycopg2.connect(
host="pg-359aec68-tugas-pendata.g.aivencloud.com",
user="avnadmin",
password="AVNS_oal2yP3mG6JLIwX3BUK",
database="defaultdb",
port=17416
)
cursor = conn.cursor()
cursor.execute("SELECT * FROM iris_data")
data = cursor.fetchall()
columns = [desc[0] for desc in cursor.description]
cursor.close()
conn.close()
return pd.DataFrame(data, columns=columns)
def get_mysql_data():
conn = pymysql.connect(
host="mysql-3634ef1a-tugas-pendata.g.aivencloud.com",
user="avnadmin",
password="AVNS_2NRSFWfr9pGMEI7BSpA",
database="defaultdb",
port=17416
)
cursor = conn.cursor()
cursor.execute("SELECT * FROM iris_data")
data = cursor.fetchall()
columns = [desc[0] for desc in cursor.description]
cursor.close()
conn.close()
return pd.DataFrame(data, columns=columns)
# Ambil data dari kedua database
df_postgresql = get_pg_data()
df_mysql = get_mysql_data()
# Gabungkan berdasarkan kolom 'id' dan 'Class'
df_merged = pd.merge(df_mysql, df_postgresql, on=["id", "class"], how="inner")
# Cetak semua data hasil gabungan tanpa indeks
print(df_merged.to_string(index=False))
id class petal_length petal_width sepal_length sepal_width
1 Iris-setosa 1.4 0.2 5.1 3.5
2 Iris-setosa 1.4 0.2 4.9 3.0
3 Iris-setosa 1.3 0.2 4.7 3.2
4 Iris-setosa 1.5 0.2 4.6 3.1
5 Iris-setosa 1.4 0.2 5.0 3.6
6 Iris-setosa 1.7 0.4 5.4 3.9
7 Iris-setosa 1.4 0.3 4.6 3.4
8 Iris-setosa 1.5 0.2 5.0 3.4
9 Iris-setosa 1.4 0.2 4.4 2.9
10 Iris-setosa 1.5 0.1 4.9 3.1
11 Iris-setosa 1.5 0.2 5.4 3.7
12 Iris-setosa 1.6 0.2 4.8 3.4
13 Iris-setosa 1.4 0.1 4.8 3.0
14 Iris-setosa 1.1 0.1 4.3 3.0
15 Iris-setosa 1.2 0.2 5.8 4.0
16 Iris-setosa 1.5 0.4 5.7 4.4
17 Iris-setosa 1.3 0.4 5.4 3.9
18 Iris-setosa 1.4 0.3 5.1 3.5
19 Iris-setosa 1.7 0.3 5.7 3.8
20 Iris-setosa 1.5 0.3 5.1 3.8
21 Iris-setosa 1.7 0.2 5.4 3.4
22 Iris-setosa 1.5 0.4 5.1 3.7
23 Iris-setosa 1.0 0.2 4.6 3.6
24 Iris-setosa 1.7 0.5 5.1 3.3
25 Iris-setosa 1.9 0.2 4.8 3.4
26 Iris-setosa 1.6 0.2 5.0 3.0
27 Iris-setosa 1.6 0.4 5.0 3.4
28 Iris-setosa 1.5 0.2 5.2 3.5
29 Iris-setosa 1.4 0.2 5.2 3.4
30 Iris-setosa 1.6 0.2 4.7 3.2
31 Iris-setosa 1.6 0.2 4.8 3.1
32 Iris-setosa 1.5 0.4 5.4 3.4
33 Iris-setosa 1.5 0.1 5.2 4.1
34 Iris-setosa 1.4 0.2 5.5 4.2
35 Iris-setosa 1.5 0.1 4.9 3.1
36 Iris-setosa 1.2 0.2 5.0 3.2
37 Iris-setosa 1.3 0.2 5.5 3.5
38 Iris-setosa 1.5 0.1 4.9 3.1
39 Iris-setosa 1.3 0.2 4.4 3.0
40 Iris-setosa 1.5 0.2 5.1 3.4
41 Iris-setosa 1.3 0.3 5.0 3.5
42 Iris-setosa 1.3 0.3 4.5 2.3
43 Iris-setosa 1.3 0.2 4.4 3.2
44 Iris-setosa 1.6 0.6 5.0 3.5
45 Iris-setosa 1.9 0.4 5.1 3.8
46 Iris-setosa 1.4 0.3 4.8 3.0
47 Iris-setosa 1.6 0.2 5.1 3.8
48 Iris-setosa 1.4 0.2 4.6 3.2
49 Iris-setosa 1.5 0.2 5.3 3.7
50 Iris-setosa 1.4 0.2 5.0 3.3
51 Iris-versicolor 4.7 1.4 7.0 3.2
52 Iris-versicolor 4.5 1.5 6.4 3.2
53 Iris-versicolor 4.9 1.5 6.9 3.1
54 Iris-versicolor 4.0 1.3 5.5 2.3
55 Iris-versicolor 4.6 1.5 6.5 2.8
56 Iris-versicolor 4.5 1.3 5.7 2.8
57 Iris-versicolor 4.7 1.6 6.3 3.3
58 Iris-versicolor 3.3 1.0 4.9 2.4
59 Iris-versicolor 4.6 1.3 6.6 2.9
60 Iris-versicolor 3.9 1.4 5.2 2.7
61 Iris-versicolor 3.5 1.0 5.0 2.0
62 Iris-versicolor 4.2 1.5 5.9 3.0
63 Iris-versicolor 4.0 1.0 6.0 2.2
64 Iris-versicolor 4.7 1.4 6.1 2.9
65 Iris-versicolor 3.6 1.3 5.6 2.9
66 Iris-versicolor 4.4 1.4 6.7 3.1
67 Iris-versicolor 4.5 1.5 5.6 3.0
68 Iris-versicolor 4.1 1.0 5.8 2.7
69 Iris-versicolor 4.5 1.5 6.2 2.2
70 Iris-versicolor 3.9 1.1 5.6 2.5
71 Iris-versicolor 4.8 1.8 5.9 3.2
72 Iris-versicolor 4.0 1.3 6.1 2.8
73 Iris-versicolor 4.9 1.5 6.3 2.5
74 Iris-versicolor 4.7 1.2 6.1 2.8
75 Iris-versicolor 4.3 1.3 6.4 2.9
76 Iris-versicolor 4.4 1.4 6.6 3.0
77 Iris-versicolor 4.8 1.4 6.8 2.8
78 Iris-versicolor 5.0 1.7 6.7 3.0
79 Iris-versicolor 4.5 1.5 6.0 2.9
80 Iris-versicolor 3.5 1.0 5.7 2.6
81 Iris-versicolor 3.8 1.1 5.5 2.4
82 Iris-versicolor 3.7 1.0 5.5 2.4
83 Iris-versicolor 3.9 1.2 5.8 2.7
84 Iris-versicolor 5.1 1.6 6.0 2.7
85 Iris-versicolor 4.5 1.5 5.4 3.0
86 Iris-versicolor 4.5 1.6 6.0 3.4
87 Iris-versicolor 4.7 1.5 6.7 3.1
88 Iris-versicolor 4.4 1.3 6.3 2.3
89 Iris-versicolor 4.1 1.3 5.6 3.0
90 Iris-versicolor 4.0 1.3 5.5 2.5
91 Iris-versicolor 4.4 1.2 5.5 2.6
92 Iris-versicolor 4.6 1.4 6.1 3.0
93 Iris-versicolor 4.0 1.2 5.8 2.6
94 Iris-versicolor 3.3 1.0 5.0 2.3
95 Iris-versicolor 4.2 1.3 5.6 2.7
96 Iris-versicolor 4.2 1.2 5.7 3.0
97 Iris-versicolor 4.2 1.3 5.7 2.9
98 Iris-versicolor 4.3 1.3 6.2 2.9
99 Iris-versicolor 3.0 1.1 5.1 2.5
100 Iris-versicolor 4.1 1.3 5.7 2.8
101 Iris-virginica 6.0 2.5 6.3 3.3
102 Iris-virginica 5.1 1.9 5.8 2.7
103 Iris-virginica 5.9 2.1 7.1 3.0
104 Iris-virginica 5.6 1.8 6.3 2.9
105 Iris-virginica 5.8 2.2 6.5 3.0
106 Iris-virginica 6.6 2.1 7.6 3.0
107 Iris-virginica 4.5 1.7 4.9 2.5
108 Iris-virginica 6.3 1.8 7.3 2.9
109 Iris-virginica 5.8 1.8 6.7 2.5
110 Iris-virginica 6.1 2.5 7.2 3.6
111 Iris-virginica 5.1 2.0 6.5 3.2
112 Iris-virginica 5.3 1.9 6.4 2.7
113 Iris-virginica 5.5 2.1 6.8 3.0
114 Iris-virginica 5.0 2.0 5.7 2.5
115 Iris-virginica 5.1 2.4 5.8 2.8
116 Iris-virginica 5.3 2.3 6.4 3.2
117 Iris-virginica 5.5 1.8 6.5 3.0
118 Iris-virginica 6.7 2.2 7.7 3.8
119 Iris-virginica 6.9 2.3 7.7 2.6
120 Iris-virginica 5.0 1.5 6.0 2.2
121 Iris-virginica 5.7 2.3 6.9 3.2
122 Iris-virginica 4.9 2.0 5.6 2.8
123 Iris-virginica 6.7 2.0 7.7 2.8
124 Iris-virginica 4.9 1.8 6.3 2.7
125 Iris-virginica 5.7 2.1 6.7 3.3
126 Iris-virginica 6.0 1.8 7.2 3.2
127 Iris-virginica 4.8 1.8 6.2 2.8
128 Iris-virginica 4.9 1.8 6.1 3.0
129 Iris-virginica 5.6 2.1 6.4 2.8
130 Iris-virginica 5.8 1.6 7.2 3.0
131 Iris-virginica 6.1 1.9 7.4 2.8
132 Iris-virginica 6.4 2.0 7.9 3.8
133 Iris-virginica 5.6 2.2 6.4 2.8
134 Iris-virginica 5.1 1.5 6.3 2.8
135 Iris-virginica 5.6 1.4 6.1 2.6
136 Iris-virginica 6.1 2.3 7.7 3.0
137 Iris-virginica 5.6 2.4 6.3 3.4
138 Iris-virginica 5.5 1.8 6.4 3.1
139 Iris-virginica 4.8 1.8 6.0 3.0
140 Iris-virginica 5.4 2.1 6.9 3.1
141 Iris-virginica 5.6 2.4 6.7 3.1
142 Iris-virginica 5.1 2.3 6.9 3.1
143 Iris-virginica 5.1 1.9 5.8 2.7
144 Iris-virginica 5.9 2.3 6.8 3.2
145 Iris-virginica 5.7 2.5 6.7 3.3
146 Iris-virginica 5.2 2.3 6.7 3.0
147 Iris-virginica 5.0 1.9 6.3 2.5
148 Iris-virginica 5.2 2.0 6.5 3.0
149 Iris-virginica 5.4 2.3 6.2 3.4
150 Iris-virginica 5.1 1.8 5.9 3.0
Data Asli Sebelum Normalisasi#
# Ambil hanya fitur numerik (hapus kolom non-numerik)
features_before_scaling = df_merged.drop(columns=['id', 'class'])
print (features_before_scaling.to_string(index=False));
petal_length petal_width sepal_length sepal_width
1.4 0.2 5.1 3.5
1.4 0.2 4.9 3.0
1.3 0.2 4.7 3.2
1.5 0.2 4.6 3.1
1.4 0.2 5.0 3.6
1.7 0.4 5.4 3.9
1.4 0.3 4.6 3.4
1.5 0.2 5.0 3.4
1.4 0.2 4.4 2.9
1.5 0.1 4.9 3.1
1.5 0.2 5.4 3.7
1.6 0.2 4.8 3.4
1.4 0.1 4.8 3.0
1.1 0.1 4.3 3.0
1.2 0.2 5.8 4.0
1.5 0.4 5.7 4.4
1.3 0.4 5.4 3.9
1.4 0.3 5.1 3.5
1.7 0.3 5.7 3.8
1.5 0.3 5.1 3.8
1.7 0.2 5.4 3.4
1.5 0.4 5.1 3.7
1.0 0.2 4.6 3.6
1.7 0.5 5.1 3.3
1.9 0.2 4.8 3.4
1.6 0.2 5.0 3.0
1.6 0.4 5.0 3.4
1.5 0.2 5.2 3.5
1.4 0.2 5.2 3.4
1.6 0.2 4.7 3.2
1.6 0.2 4.8 3.1
1.5 0.4 5.4 3.4
1.5 0.1 5.2 4.1
1.4 0.2 5.5 4.2
1.5 0.1 4.9 3.1
1.2 0.2 5.0 3.2
1.3 0.2 5.5 3.5
1.5 0.1 4.9 3.1
1.3 0.2 4.4 3.0
1.5 0.2 5.1 3.4
1.3 0.3 5.0 3.5
1.3 0.3 4.5 2.3
1.3 0.2 4.4 3.2
1.6 0.6 5.0 3.5
1.9 0.4 5.1 3.8
1.4 0.3 4.8 3.0
1.6 0.2 5.1 3.8
1.4 0.2 4.6 3.2
1.5 0.2 5.3 3.7
1.4 0.2 5.0 3.3
4.7 1.4 7.0 3.2
4.5 1.5 6.4 3.2
4.9 1.5 6.9 3.1
4.0 1.3 5.5 2.3
4.6 1.5 6.5 2.8
4.5 1.3 5.7 2.8
4.7 1.6 6.3 3.3
3.3 1.0 4.9 2.4
4.6 1.3 6.6 2.9
3.9 1.4 5.2 2.7
3.5 1.0 5.0 2.0
4.2 1.5 5.9 3.0
4.0 1.0 6.0 2.2
4.7 1.4 6.1 2.9
3.6 1.3 5.6 2.9
4.4 1.4 6.7 3.1
4.5 1.5 5.6 3.0
4.1 1.0 5.8 2.7
4.5 1.5 6.2 2.2
3.9 1.1 5.6 2.5
4.8 1.8 5.9 3.2
4.0 1.3 6.1 2.8
4.9 1.5 6.3 2.5
4.7 1.2 6.1 2.8
4.3 1.3 6.4 2.9
4.4 1.4 6.6 3.0
4.8 1.4 6.8 2.8
5.0 1.7 6.7 3.0
4.5 1.5 6.0 2.9
3.5 1.0 5.7 2.6
3.8 1.1 5.5 2.4
3.7 1.0 5.5 2.4
3.9 1.2 5.8 2.7
5.1 1.6 6.0 2.7
4.5 1.5 5.4 3.0
4.5 1.6 6.0 3.4
4.7 1.5 6.7 3.1
4.4 1.3 6.3 2.3
4.1 1.3 5.6 3.0
4.0 1.3 5.5 2.5
4.4 1.2 5.5 2.6
4.6 1.4 6.1 3.0
4.0 1.2 5.8 2.6
3.3 1.0 5.0 2.3
4.2 1.3 5.6 2.7
4.2 1.2 5.7 3.0
4.2 1.3 5.7 2.9
4.3 1.3 6.2 2.9
3.0 1.1 5.1 2.5
4.1 1.3 5.7 2.8
6.0 2.5 6.3 3.3
5.1 1.9 5.8 2.7
5.9 2.1 7.1 3.0
5.6 1.8 6.3 2.9
5.8 2.2 6.5 3.0
6.6 2.1 7.6 3.0
4.5 1.7 4.9 2.5
6.3 1.8 7.3 2.9
5.8 1.8 6.7 2.5
6.1 2.5 7.2 3.6
5.1 2.0 6.5 3.2
5.3 1.9 6.4 2.7
5.5 2.1 6.8 3.0
5.0 2.0 5.7 2.5
5.1 2.4 5.8 2.8
5.3 2.3 6.4 3.2
5.5 1.8 6.5 3.0
6.7 2.2 7.7 3.8
6.9 2.3 7.7 2.6
5.0 1.5 6.0 2.2
5.7 2.3 6.9 3.2
4.9 2.0 5.6 2.8
6.7 2.0 7.7 2.8
4.9 1.8 6.3 2.7
5.7 2.1 6.7 3.3
6.0 1.8 7.2 3.2
4.8 1.8 6.2 2.8
4.9 1.8 6.1 3.0
5.6 2.1 6.4 2.8
5.8 1.6 7.2 3.0
6.1 1.9 7.4 2.8
6.4 2.0 7.9 3.8
5.6 2.2 6.4 2.8
5.1 1.5 6.3 2.8
5.6 1.4 6.1 2.6
6.1 2.3 7.7 3.0
5.6 2.4 6.3 3.4
5.5 1.8 6.4 3.1
4.8 1.8 6.0 3.0
5.4 2.1 6.9 3.1
5.6 2.4 6.7 3.1
5.1 2.3 6.9 3.1
5.1 1.9 5.8 2.7
5.9 2.3 6.8 3.2
5.7 2.5 6.7 3.3
5.2 2.3 6.7 3.0
5.0 1.9 6.3 2.5
5.2 2.0 6.5 3.0
5.4 2.3 6.2 3.4
5.1 1.8 5.9 3.0
Visualisasi Data#
Visualisasi data asli tanpa menggunakan PCA#
Ini adalah visualisasi data Iris secara 2 Dimensi tanpa menggunakan PCA
# Ubah kolom 'class' menjadi kategori jika belum
df_merged['class'] = df_merged['class'].astype('category')
# Plot 2D scatter plot
plt.figure(figsize=(8, 6))
for label in df_merged['class'].cat.categories:
subset = df_merged[df_merged['class'] == label]
plt.scatter(subset['sepal_length'], subset['sepal_width'], label=label, s=80, edgecolors='k')
plt.title("Visualisasi 2D Data Iris")
plt.xlabel("Sepal Length")
plt.ylabel("Sepal Width")
plt.legend(title='Class')
plt.grid(True)
plt.show()
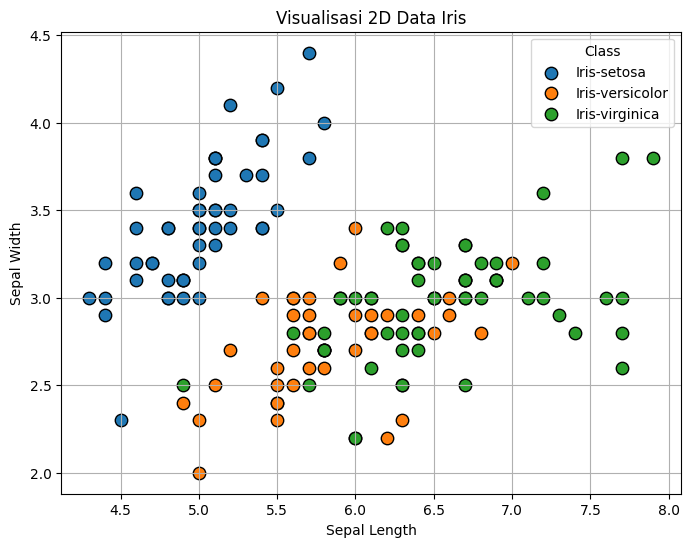
Ini adalah visualisasi data Iris secara 3 Dimensi tanpa menggunakan PCA
df_merged['class'] = df_merged['class'].astype('category')
# Plot 3D scatter plot
fig = plt.figure(figsize=(10, 7))
ax = fig.add_subplot(111, projection='3d')
for label in df_merged['class'].cat.categories:
subset = df_merged[df_merged['class'] == label]
ax.scatter(
subset['sepal_length'],
subset['sepal_width'],
subset['petal_length'],
label=label,
s=80,
edgecolors='k'
)
ax.set_title("Visualisasi 3D Data Iris")
ax.set_xlabel("Sepal Length")
ax.set_ylabel("Sepal Width")
ax.set_zlabel("Petal Length")
ax.legend(title='Class')
plt.tight_layout()
plt.show()
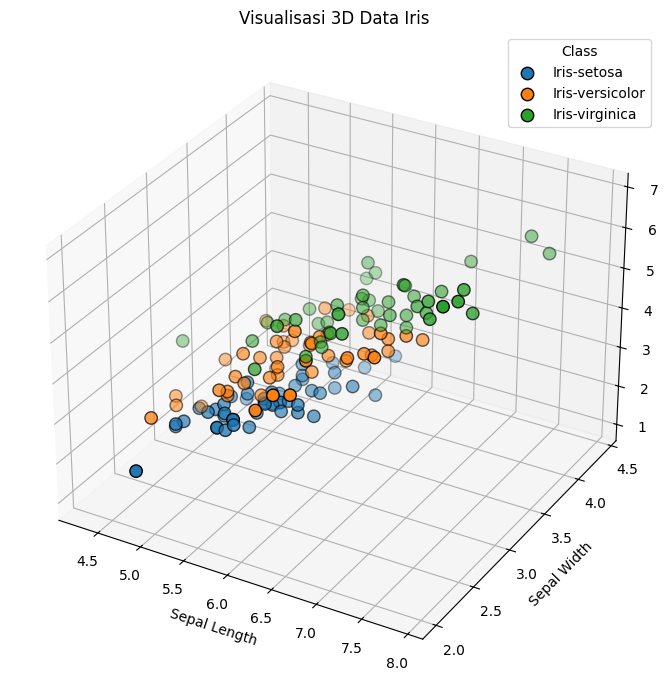
Visualisasi data asli menggunakan PCA#
Ini adalah visualisasi data Iris secara 2 Dimensi menggunakan PCA
# Ambil hanya fitur numerik (hapus kolom non-numerik)
features_before_scaling = df_merged.drop(columns=['id', 'class'])
# PCA langsung pada data mentah (belum dinormalisasi)
pca_raw = PCA(n_components=2)
reduced_raw = pca_raw.fit_transform(features_before_scaling)
# Visualisasi 2D hasil PCA sebelum normalisasi
plt.figure(figsize=(6, 4))
plt.scatter(reduced_raw[:, 0], reduced_raw[:, 1], c='blue', s=50, alpha=0.7)
plt.title("Visualisasi PCA 2D Data Iris")
plt.xlabel("PCA 1")
plt.ylabel("PCA 2")
plt.grid(True)
plt.show()
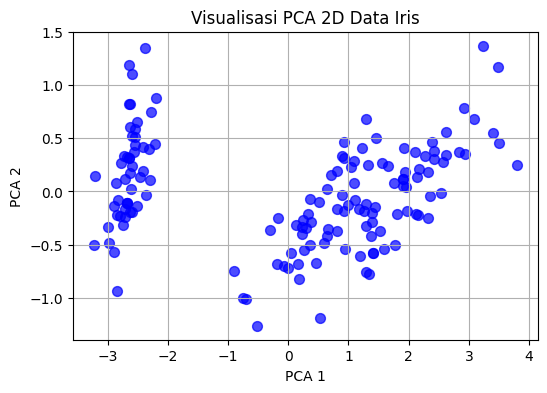
Ini adalah visualisasi data Iris secara 3 Dimensi menggunakan PCA
# Ambil hanya fitur numerik (hapus kolom non-numerik)
features_before_scaling = df_merged.drop(columns=['id', 'class'])
# PCA ke 3 komponen tanpa normalisasi
pca_raw_3d = PCA(n_components=3)
reduced_raw_3d = pca_raw_3d.fit_transform(features_before_scaling)
# Visualisasi 3D hasil PCA sebelum normalisasi
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(
reduced_raw_3d[:, 0],
reduced_raw_3d[:, 1],
reduced_raw_3d[:, 2],
c='blue',
s=50,
alpha=0.7
)
ax.set_title("Visualisasi PCA 3D Data Iris")
ax.set_xlabel("PCA 1")
ax.set_ylabel("PCA 2")
ax.set_zlabel("PCA 3")
plt.grid(True)
plt.tight_layout()
plt.show()
Normalisasi menggunakan Min-Max#
Min-Max Normalization (skala min-maks) adalah metode untuk menyelaraskan skala semua fitur numerik ke dalam rentang tertentu, biasanya antara 0 dan 1.
Tujuan Min-Max Scaling:
Menstandarkan skala fitur:
Data seperti panjang kelopak bisa bernilai 1–7, sedangkan lebar sepal mungkin 0.1–1.5 → ini membuat model seperti K-Means atau KNN lebih berat ke fitur yang besar.
Dengan skala seragam (0–1), semua fitur punya kontribusi yang seimbang.
Meningkatkan performa algoritma:
Model berbasis jarak (misalnya K-Means, K-Nearest Neighbors, PCA) sangat terpengaruh oleh skala fitur.
Min-Max membantu hasil yang lebih stabil dan akurat.
Mempercepat konvergensi model:
Dalam algoritma iteratif (seperti K-Means), normalisasi membuat proses training lebih cepat dan efisien.
from sklearn.preprocessing import MinMaxScaler
# 1. Pilih kolom numerik saja (kecuali 'id' dan 'class')
numerical_cols = df_merged.select_dtypes(include=['float64', 'int64']).columns
numerical_cols = [col for col in numerical_cols if col not in ['id']] # abaikan 'id'
# 2. Inisialisasi scaler
scaler = MinMaxScaler()
# 3. Lakukan normalisasi
df_normalized = df_merged.copy()
df_normalized[numerical_cols] = scaler.fit_transform(df_merged[numerical_cols])
# 4. Cetak hasil setelah normalisasi
print("\nData setelah normalisasi (Min-Max):")
print(df_normalized.to_string(index=False))
Data setelah normalisasi (Min-Max):
id class petal_length petal_width sepal_length sepal_width
1 Iris-setosa 0.067797 0.041667 0.222222 0.625000
2 Iris-setosa 0.067797 0.041667 0.166667 0.416667
3 Iris-setosa 0.050847 0.041667 0.111111 0.500000
4 Iris-setosa 0.084746 0.041667 0.083333 0.458333
5 Iris-setosa 0.067797 0.041667 0.194444 0.666667
6 Iris-setosa 0.118644 0.125000 0.305556 0.791667
7 Iris-setosa 0.067797 0.083333 0.083333 0.583333
8 Iris-setosa 0.084746 0.041667 0.194444 0.583333
9 Iris-setosa 0.067797 0.041667 0.027778 0.375000
10 Iris-setosa 0.084746 0.000000 0.166667 0.458333
11 Iris-setosa 0.084746 0.041667 0.305556 0.708333
12 Iris-setosa 0.101695 0.041667 0.138889 0.583333
13 Iris-setosa 0.067797 0.000000 0.138889 0.416667
14 Iris-setosa 0.016949 0.000000 0.000000 0.416667
15 Iris-setosa 0.033898 0.041667 0.416667 0.833333
16 Iris-setosa 0.084746 0.125000 0.388889 1.000000
17 Iris-setosa 0.050847 0.125000 0.305556 0.791667
18 Iris-setosa 0.067797 0.083333 0.222222 0.625000
19 Iris-setosa 0.118644 0.083333 0.388889 0.750000
20 Iris-setosa 0.084746 0.083333 0.222222 0.750000
21 Iris-setosa 0.118644 0.041667 0.305556 0.583333
22 Iris-setosa 0.084746 0.125000 0.222222 0.708333
23 Iris-setosa 0.000000 0.041667 0.083333 0.666667
24 Iris-setosa 0.118644 0.166667 0.222222 0.541667
25 Iris-setosa 0.152542 0.041667 0.138889 0.583333
26 Iris-setosa 0.101695 0.041667 0.194444 0.416667
27 Iris-setosa 0.101695 0.125000 0.194444 0.583333
28 Iris-setosa 0.084746 0.041667 0.250000 0.625000
29 Iris-setosa 0.067797 0.041667 0.250000 0.583333
30 Iris-setosa 0.101695 0.041667 0.111111 0.500000
31 Iris-setosa 0.101695 0.041667 0.138889 0.458333
32 Iris-setosa 0.084746 0.125000 0.305556 0.583333
33 Iris-setosa 0.084746 0.000000 0.250000 0.875000
34 Iris-setosa 0.067797 0.041667 0.333333 0.916667
35 Iris-setosa 0.084746 0.000000 0.166667 0.458333
36 Iris-setosa 0.033898 0.041667 0.194444 0.500000
37 Iris-setosa 0.050847 0.041667 0.333333 0.625000
38 Iris-setosa 0.084746 0.000000 0.166667 0.458333
39 Iris-setosa 0.050847 0.041667 0.027778 0.416667
40 Iris-setosa 0.084746 0.041667 0.222222 0.583333
41 Iris-setosa 0.050847 0.083333 0.194444 0.625000
42 Iris-setosa 0.050847 0.083333 0.055556 0.125000
43 Iris-setosa 0.050847 0.041667 0.027778 0.500000
44 Iris-setosa 0.101695 0.208333 0.194444 0.625000
45 Iris-setosa 0.152542 0.125000 0.222222 0.750000
46 Iris-setosa 0.067797 0.083333 0.138889 0.416667
47 Iris-setosa 0.101695 0.041667 0.222222 0.750000
48 Iris-setosa 0.067797 0.041667 0.083333 0.500000
49 Iris-setosa 0.084746 0.041667 0.277778 0.708333
50 Iris-setosa 0.067797 0.041667 0.194444 0.541667
51 Iris-versicolor 0.627119 0.541667 0.750000 0.500000
52 Iris-versicolor 0.593220 0.583333 0.583333 0.500000
53 Iris-versicolor 0.661017 0.583333 0.722222 0.458333
54 Iris-versicolor 0.508475 0.500000 0.333333 0.125000
55 Iris-versicolor 0.610169 0.583333 0.611111 0.333333
56 Iris-versicolor 0.593220 0.500000 0.388889 0.333333
57 Iris-versicolor 0.627119 0.625000 0.555556 0.541667
58 Iris-versicolor 0.389831 0.375000 0.166667 0.166667
59 Iris-versicolor 0.610169 0.500000 0.638889 0.375000
60 Iris-versicolor 0.491525 0.541667 0.250000 0.291667
61 Iris-versicolor 0.423729 0.375000 0.194444 0.000000
62 Iris-versicolor 0.542373 0.583333 0.444444 0.416667
63 Iris-versicolor 0.508475 0.375000 0.472222 0.083333
64 Iris-versicolor 0.627119 0.541667 0.500000 0.375000
65 Iris-versicolor 0.440678 0.500000 0.361111 0.375000
66 Iris-versicolor 0.576271 0.541667 0.666667 0.458333
67 Iris-versicolor 0.593220 0.583333 0.361111 0.416667
68 Iris-versicolor 0.525424 0.375000 0.416667 0.291667
69 Iris-versicolor 0.593220 0.583333 0.527778 0.083333
70 Iris-versicolor 0.491525 0.416667 0.361111 0.208333
71 Iris-versicolor 0.644068 0.708333 0.444444 0.500000
72 Iris-versicolor 0.508475 0.500000 0.500000 0.333333
73 Iris-versicolor 0.661017 0.583333 0.555556 0.208333
74 Iris-versicolor 0.627119 0.458333 0.500000 0.333333
75 Iris-versicolor 0.559322 0.500000 0.583333 0.375000
76 Iris-versicolor 0.576271 0.541667 0.638889 0.416667
77 Iris-versicolor 0.644068 0.541667 0.694444 0.333333
78 Iris-versicolor 0.677966 0.666667 0.666667 0.416667
79 Iris-versicolor 0.593220 0.583333 0.472222 0.375000
80 Iris-versicolor 0.423729 0.375000 0.388889 0.250000
81 Iris-versicolor 0.474576 0.416667 0.333333 0.166667
82 Iris-versicolor 0.457627 0.375000 0.333333 0.166667
83 Iris-versicolor 0.491525 0.458333 0.416667 0.291667
84 Iris-versicolor 0.694915 0.625000 0.472222 0.291667
85 Iris-versicolor 0.593220 0.583333 0.305556 0.416667
86 Iris-versicolor 0.593220 0.625000 0.472222 0.583333
87 Iris-versicolor 0.627119 0.583333 0.666667 0.458333
88 Iris-versicolor 0.576271 0.500000 0.555556 0.125000
89 Iris-versicolor 0.525424 0.500000 0.361111 0.416667
90 Iris-versicolor 0.508475 0.500000 0.333333 0.208333
91 Iris-versicolor 0.576271 0.458333 0.333333 0.250000
92 Iris-versicolor 0.610169 0.541667 0.500000 0.416667
93 Iris-versicolor 0.508475 0.458333 0.416667 0.250000
94 Iris-versicolor 0.389831 0.375000 0.194444 0.125000
95 Iris-versicolor 0.542373 0.500000 0.361111 0.291667
96 Iris-versicolor 0.542373 0.458333 0.388889 0.416667
97 Iris-versicolor 0.542373 0.500000 0.388889 0.375000
98 Iris-versicolor 0.559322 0.500000 0.527778 0.375000
99 Iris-versicolor 0.338983 0.416667 0.222222 0.208333
100 Iris-versicolor 0.525424 0.500000 0.388889 0.333333
101 Iris-virginica 0.847458 1.000000 0.555556 0.541667
102 Iris-virginica 0.694915 0.750000 0.416667 0.291667
103 Iris-virginica 0.830508 0.833333 0.777778 0.416667
104 Iris-virginica 0.779661 0.708333 0.555556 0.375000
105 Iris-virginica 0.813559 0.875000 0.611111 0.416667
106 Iris-virginica 0.949153 0.833333 0.916667 0.416667
107 Iris-virginica 0.593220 0.666667 0.166667 0.208333
108 Iris-virginica 0.898305 0.708333 0.833333 0.375000
109 Iris-virginica 0.813559 0.708333 0.666667 0.208333
110 Iris-virginica 0.864407 1.000000 0.805556 0.666667
111 Iris-virginica 0.694915 0.791667 0.611111 0.500000
112 Iris-virginica 0.728814 0.750000 0.583333 0.291667
113 Iris-virginica 0.762712 0.833333 0.694444 0.416667
114 Iris-virginica 0.677966 0.791667 0.388889 0.208333
115 Iris-virginica 0.694915 0.958333 0.416667 0.333333
116 Iris-virginica 0.728814 0.916667 0.583333 0.500000
117 Iris-virginica 0.762712 0.708333 0.611111 0.416667
118 Iris-virginica 0.966102 0.875000 0.944444 0.750000
119 Iris-virginica 1.000000 0.916667 0.944444 0.250000
120 Iris-virginica 0.677966 0.583333 0.472222 0.083333
121 Iris-virginica 0.796610 0.916667 0.722222 0.500000
122 Iris-virginica 0.661017 0.791667 0.361111 0.333333
123 Iris-virginica 0.966102 0.791667 0.944444 0.333333
124 Iris-virginica 0.661017 0.708333 0.555556 0.291667
125 Iris-virginica 0.796610 0.833333 0.666667 0.541667
126 Iris-virginica 0.847458 0.708333 0.805556 0.500000
127 Iris-virginica 0.644068 0.708333 0.527778 0.333333
128 Iris-virginica 0.661017 0.708333 0.500000 0.416667
129 Iris-virginica 0.779661 0.833333 0.583333 0.333333
130 Iris-virginica 0.813559 0.625000 0.805556 0.416667
131 Iris-virginica 0.864407 0.750000 0.861111 0.333333
132 Iris-virginica 0.915254 0.791667 1.000000 0.750000
133 Iris-virginica 0.779661 0.875000 0.583333 0.333333
134 Iris-virginica 0.694915 0.583333 0.555556 0.333333
135 Iris-virginica 0.779661 0.541667 0.500000 0.250000
136 Iris-virginica 0.864407 0.916667 0.944444 0.416667
137 Iris-virginica 0.779661 0.958333 0.555556 0.583333
138 Iris-virginica 0.762712 0.708333 0.583333 0.458333
139 Iris-virginica 0.644068 0.708333 0.472222 0.416667
140 Iris-virginica 0.745763 0.833333 0.722222 0.458333
141 Iris-virginica 0.779661 0.958333 0.666667 0.458333
142 Iris-virginica 0.694915 0.916667 0.722222 0.458333
143 Iris-virginica 0.694915 0.750000 0.416667 0.291667
144 Iris-virginica 0.830508 0.916667 0.694444 0.500000
145 Iris-virginica 0.796610 1.000000 0.666667 0.541667
146 Iris-virginica 0.711864 0.916667 0.666667 0.416667
147 Iris-virginica 0.677966 0.750000 0.555556 0.208333
148 Iris-virginica 0.711864 0.791667 0.611111 0.416667
149 Iris-virginica 0.745763 0.916667 0.527778 0.583333
150 Iris-virginica 0.694915 0.708333 0.444444 0.416667
Reduksi DImensi#
Apa Itu Reduksi Dimensi?#
Reduksi dimensi adalah proses menyederhanakan data dengan mengurangi jumlah fitur (kolom) sambil tetap mempertahankan informasi penting sebanyak mungkin.
Tujuan Reduksi Dimensi:#
Mengurangi Kompleksitas: Data dengan banyak fitur (misalnya 100 kolom) bisa rumit untuk diproses:
Mempercepat Komputasi: Lebih sedikit fitur = proses training lebih cepat.
Meningkatkan Visualisasi: Data bisa divisualisasikan dalam 2D atau 3D.
Mengurangi Overfitting: Fitur berlebih bisa menyebabkan model terlalu menyesuaikan data.
Menghilangkan Redundansi: Fitur yang mirip (berkorelasi) digabungkan menjadi fitur baru.
from sklearn.decomposition import PCA
# 1. Ambil hanya fitur numerik yang sudah dinormalisasi (tanpa 'id' dan 'class')
X = df_normalized[numerical_cols].values
# 2. Inisialisasi PCA untuk reduksi ke 2D dan 3D
pca_2d = PCA(n_components=2)
X_pca_2d = pca_2d.fit_transform(X)
pca_3d = PCA(n_components=3)
X_pca_3d = pca_3d.fit_transform(X)
# 3. Buat DataFrame hasil reduksi dimensi
df_pca_2d = pd.DataFrame(X_pca_2d, columns=['PC1', 'PC2'])
df_pca_3d = pd.DataFrame(X_pca_3d, columns=['PC1', 'PC2', 'PC3'])
# 4. Gabungkan kembali dengan kolom 'id' dan 'class' untuk referensi
df_pca_2d['id'] = df_normalized['id'].values
df_pca_2d['class'] = df_normalized['class'].values
df_pca_3d['id'] = df_normalized['id'].values
df_pca_3d['class'] = df_normalized['class'].values
# 5. Tampilkan hasil
print("\nHasil PCA 2D:")
print(df_pca_2d.to_string(index=False))
print("\nHasil PCA 3D:")
print(df_pca_3d.to_string(index=False))
Hasil PCA 2D:
PC1 PC2 id class
-0.630361 0.111556 1 Iris-setosa
-0.623546 -0.100313 2 Iris-setosa
-0.669793 -0.047220 3 Iris-setosa
-0.654633 -0.098791 4 Iris-setosa
-0.648263 0.137558 5 Iris-setosa
-0.534057 0.293223 6 Iris-setosa
-0.656396 0.014922 7 Iris-setosa
-0.625644 0.061075 8 Iris-setosa
-0.676526 -0.196482 9 Iris-setosa
-0.646137 -0.063242 10 Iris-setosa
-0.596655 0.220942 11 Iris-setosa
-0.638829 0.036596 12 Iris-setosa
-0.662305 -0.111543 13 Iris-setosa
-0.752700 -0.166745 14 Iris-setosa
-0.598993 0.384079 15 Iris-setosa
-0.549943 0.518968 16 Iris-setosa
-0.575827 0.297584 17 Iris-setosa
-0.603416 0.111091 18 Iris-setosa
-0.519473 0.291076 19 Iris-setosa
-0.611239 0.223089 20 Iris-setosa
-0.557505 0.105673 21 Iris-setosa
-0.578206 0.184928 22 Iris-setosa
-0.737287 0.095140 23 Iris-setosa
-0.506022 0.031498 24 Iris-setosa
-0.607501 0.033325 25 Iris-setosa
-0.590848 -0.090799 26 Iris-setosa
-0.561312 0.059055 27 Iris-setosa
-0.608105 0.122161 28 Iris-setosa
-0.612459 0.085555 29 Iris-setosa
-0.638465 -0.050491 30 Iris-setosa
-0.620563 -0.076492 31 Iris-setosa
-0.524500 0.106923 32 Iris-setosa
-0.671581 0.348802 33 Iris-setosa
-0.625726 0.422207 34 Iris-setosa
-0.646137 -0.063242 35 Iris-setosa
-0.644794 -0.011046 36 Iris-setosa
-0.593549 0.159425 37 Iris-setosa
-0.646137 -0.063242 38 Iris-setosa
-0.693057 -0.157696 39 Iris-setosa
-0.613830 0.072770 40 Iris-setosa
-0.625672 0.100487 41 Iris-setosa
-0.611679 -0.410339 42 Iris-setosa
-0.705234 -0.082304 43 Iris-setosa
-0.513510 0.095820 44 Iris-setosa
-0.542524 0.218263 45 Iris-setosa
-0.608415 -0.112473 46 Iris-setosa
-0.627742 0.222464 47 Iris-setosa
-0.671164 -0.060005 48 Iris-setosa
-0.608468 0.209247 49 Iris-setosa
-0.629998 0.024470 50 Iris-setosa
0.280302 0.179104 51 Iris-versicolor
0.215481 0.110652 52 Iris-versicolor
0.322407 0.127068 53 Iris-versicolor
0.057852 -0.327482 54 Iris-versicolor
0.262090 -0.029528 55 Iris-versicolor
0.103249 -0.121064 56 Iris-versicolor
0.245408 0.134008 57 Iris-versicolor
-0.173050 -0.350926 58 Iris-versicolor
0.213926 0.020793 59 Iris-versicolor
0.014560 -0.211157 60 Iris-versicolor
-0.115998 -0.492197 61 Iris-versicolor
0.137262 -0.019942 62 Iris-versicolor
0.042174 -0.305310 63 Iris-versicolor
0.192245 -0.039235 64 Iris-versicolor
-0.008635 -0.085250 65 Iris-versicolor
0.219622 0.109595 66 Iris-versicolor
0.133149 -0.058297 67 Iris-versicolor
-0.001453 -0.141309 68 Iris-versicolor
0.252738 -0.289698 69 Iris-versicolor
-0.006843 -0.238375 70 Iris-versicolor
0.268575 0.047512 71 Iris-versicolor
0.098291 -0.068834 72 Iris-versicolor
0.288056 -0.169276 73 Iris-versicolor
0.144444 -0.076001 74 Iris-versicolor
0.158971 0.000675 75 Iris-versicolor
0.213897 0.060204 76 Iris-versicolor
0.291471 0.003840 77 Iris-versicolor
0.369200 0.063962 78 Iris-versicolor
0.186492 -0.049215 79 Iris-versicolor
-0.069833 -0.184158 80 Iris-versicolor
-0.023011 -0.286675 81 Iris-versicolor
-0.060398 -0.285120 82 Iris-versicolor
0.031552 -0.140059 83 Iris-versicolor
0.288268 -0.131614 84 Iris-versicolor
0.109522 -0.081686 85 Iris-versicolor
0.182994 0.138800 86 Iris-versicolor
0.277895 0.105859 87 Iris-versicolor
0.194131 -0.238287 88 Iris-versicolor
0.037489 -0.053006 89 Iris-versicolor
0.045675 -0.252090 90 Iris-versicolor
0.054412 -0.218290 91 Iris-versicolor
0.175714 -0.000449 92 Iris-versicolor
0.048083 -0.178845 93 Iris-versicolor
-0.155148 -0.376928 94 Iris-versicolor
0.066197 -0.167184 95 Iris-versicolor
0.032800 -0.041936 96 Iris-versicolor
0.065834 -0.080097 97 Iris-versicolor
0.135344 -0.022715 98 Iris-versicolor
-0.159894 -0.287035 99 Iris-versicolor
0.061480 -0.116703 100 Iris-versicolor
0.623664 0.115647 101 Iris-virginica
0.345476 -0.156399 102 Iris-virginica
0.618216 0.099067 103 Iris-virginica
0.417634 -0.027520 104 Iris-virginica
0.563837 0.029524 105 Iris-virginica
0.750382 0.149908 106 Iris-virginica
0.134786 -0.329570 107 Iris-virginica
0.608867 0.081795 108 Iris-virginica
0.510127 -0.133706 109 Iris-virginica
0.722164 0.332896 110 Iris-virginica
0.424673 0.113479 111 Iris-virginica
0.437242 -0.088411 112 Iris-virginica
0.541006 0.068344 113 Iris-virginica
0.362341 -0.242860 114 Iris-virginica
0.474112 -0.121029 115 Iris-virginica
0.514579 0.098208 116 Iris-virginica
0.424730 0.034656 117 Iris-virginica
0.750875 0.461616 118 Iris-virginica
0.871766 0.006617 119 Iris-virginica
0.281323 -0.318538 120 Iris-virginica
0.615417 0.152320 121 Iris-virginica
0.321820 -0.140376 122 Iris-virginica
0.757870 0.085585 123 Iris-virginica
0.356714 -0.095280 124 Iris-virginica
0.531812 0.167557 125 Iris-virginica
0.547461 0.186459 126 Iris-virginica
0.328369 -0.068188 127 Iris-virginica
0.314821 -0.005581 128 Iris-virginica
0.516371 -0.054917 129 Iris-virginica
0.484863 0.114178 130 Iris-virginica
0.632829 0.057509 131 Iris-virginica
0.689285 0.489206 132 Iris-virginica
0.543316 -0.055382 133 Iris-virginica
0.290675 -0.058369 134 Iris-virginica
0.304493 -0.162136 135 Iris-virginica
0.763873 0.166124 136 Iris-virginica
0.548861 0.158169 137 Iris-virginica
0.406828 0.060657 138 Iris-virginica
0.292565 -0.016185 139 Iris-virginica
0.536289 0.118825 140 Iris-virginica
0.614381 0.091860 141 Iris-virginica
0.558851 0.121166 142 Iris-virginica
0.345476 -0.156399 143 Iris-virginica
0.624489 0.138445 144 Iris-virginica
0.639591 0.165696 145 Iris-virginica
0.551755 0.058990 146 Iris-virginica
0.406278 -0.172227 147 Iris-virginica
0.447293 0.036996 148 Iris-virginica
0.489218 0.149121 149 Iris-virginica
0.312079 -0.031151 150 Iris-virginica
Hasil PCA 3D:
PC1 PC2 PC3 id class
-0.630361 0.111556 0.016993 1 Iris-setosa
-0.623546 -0.100313 0.047120 2 Iris-setosa
-0.669793 -0.047220 -0.021648 3 Iris-setosa
-0.654633 -0.098791 -0.025214 4 Iris-setosa
-0.648263 0.137558 -0.016813 5 Iris-setosa
-0.534057 0.293223 -0.026736 6 Iris-setosa
-0.656396 0.014922 -0.093698 7 Iris-setosa
-0.625644 0.061075 0.012270 8 Iris-setosa
-0.676526 -0.196482 -0.038132 9 Iris-setosa
-0.646137 -0.063242 0.059754 10 Iris-setosa
-0.596655 0.220942 0.049753 11 Iris-setosa
-0.638829 0.036596 -0.026259 12 Iris-setosa
-0.662305 -0.111543 0.052716 13 Iris-setosa
-0.752700 -0.166745 -0.049969 14 Iris-setosa
-0.598993 0.384079 0.083766 15 Iris-setosa
-0.549943 0.518968 -0.039335 16 Iris-setosa
-0.575827 0.297584 -0.031364 17 Iris-setosa
-0.603416 0.111091 -0.008446 18 Iris-setosa
-0.519473 0.291076 0.072194 19 Iris-setosa
-0.611239 0.223089 -0.049177 20 Iris-setosa
-0.557505 0.105673 0.093955 21 Iris-setosa
-0.578206 0.184928 -0.060654 22 Iris-setosa
-0.737287 0.095140 -0.100812 23 Iris-setosa
-0.506022 0.031498 -0.027929 24 Iris-setosa
-0.607501 0.033325 -0.022788 25 Iris-setosa
-0.590848 -0.090799 0.069277 26 Iris-setosa
-0.561312 0.059055 -0.037452 27 Iris-setosa
-0.608105 0.122161 0.037993 28 Iris-setosa
-0.612459 0.085555 0.050798 29 Iris-setosa
-0.638465 -0.050491 -0.018177 30 Iris-setosa
-0.620563 -0.076492 0.015629 31 Iris-setosa
-0.524500 0.106923 0.040763 32 Iris-setosa
-0.671581 0.348802 -0.020344 33 Iris-setosa
-0.625726 0.422207 -0.001374 34 Iris-setosa
-0.646137 -0.063242 0.059754 35 Iris-setosa
-0.644794 -0.011046 0.036724 36 Iris-setosa
-0.593549 0.159425 0.095207 37 Iris-setosa
-0.646137 -0.063242 0.059754 38 Iris-setosa
-0.693057 -0.157696 -0.053251 39 Iris-setosa
-0.613830 0.072770 0.032112 40 Iris-setosa
-0.625672 0.100487 -0.029446 41 Iris-setosa
-0.611679 -0.410339 0.038891 42 Iris-setosa
-0.705234 -0.082304 -0.081176 43 Iris-setosa
-0.513510 0.095820 -0.102293 44 Iris-setosa
-0.542524 0.218263 -0.069989 45 Iris-setosa
-0.608415 -0.112473 0.001838 46 Iris-setosa
-0.627742 0.222464 -0.022581 47 Iris-setosa
-0.671164 -0.060005 -0.040334 48 Iris-setosa
-0.608468 0.209247 0.029910 49 Iris-setosa
-0.629998 0.024470 0.025075 50 Iris-setosa
0.280302 0.179104 0.168803 51 Iris-versicolor
0.215481 0.110652 0.021993 52 Iris-versicolor
0.322407 0.127068 0.139798 53 Iris-versicolor
0.057852 -0.327482 0.014164 54 Iris-versicolor
0.262090 -0.029528 0.098843 55 Iris-versicolor
0.103249 -0.121064 -0.010178 56 Iris-versicolor
0.245408 0.134008 -0.034938 57 Iris-versicolor
-0.173050 -0.350926 -0.050636 58 Iris-versicolor
0.213926 0.020793 0.155602 59 Iris-versicolor
0.014560 -0.211157 -0.127811 60 Iris-versicolor
-0.115998 -0.492197 0.027371 61 Iris-versicolor
0.137262 -0.019942 -0.052767 62 Iris-versicolor
0.042174 -0.305310 0.203659 63 Iris-versicolor
0.192245 -0.039235 0.032105 64 Iris-versicolor
-0.008635 -0.085250 -0.054396 65 Iris-versicolor
0.219622 0.109595 0.119767 66 Iris-versicolor
0.133149 -0.058297 -0.108825 67 Iris-versicolor
-0.001453 -0.141309 0.095317 68 Iris-versicolor
0.252738 -0.289698 0.121933 69 Iris-versicolor
-0.006843 -0.238375 0.055804 70 Iris-versicolor
0.268575 0.047512 -0.150068 71 Iris-versicolor
0.098291 -0.068834 0.063409 72 Iris-versicolor
0.288056 -0.169276 0.104516 73 Iris-versicolor
0.144444 -0.076001 0.096946 74 Iris-versicolor
0.158971 0.000675 0.112446 75 Iris-versicolor
0.213897 0.060204 0.113886 76 Iris-versicolor
0.291471 0.003840 0.186125 77 Iris-versicolor
0.369200 0.063962 0.064353 78 Iris-versicolor
0.186492 -0.049215 -0.015491 79 Iris-versicolor
-0.069833 -0.184158 0.082495 80 Iris-versicolor
-0.023011 -0.286675 0.048766 81 Iris-versicolor
-0.060398 -0.285120 0.073049 82 Iris-versicolor
0.031552 -0.140059 0.042125 83 Iris-versicolor
0.288268 -0.131614 -0.006063 84 Iris-versicolor
0.109522 -0.081686 -0.148510 85 Iris-versicolor
0.182994 0.138800 -0.110743 86 Iris-versicolor
0.277895 0.105859 0.097798 87 Iris-versicolor
0.194131 -0.238287 0.177535 88 Iris-versicolor
0.037489 -0.053006 -0.062574 89 Iris-versicolor
0.045675 -0.252090 -0.013761 90 Iris-versicolor
0.054412 -0.218290 0.002344 91 Iris-versicolor
0.175714 -0.000449 0.016986 92 Iris-versicolor
0.048083 -0.178845 0.057244 93 Iris-versicolor
-0.155148 -0.376928 -0.016831 94 Iris-versicolor
0.066197 -0.167184 -0.019529 95 Iris-versicolor
0.032800 -0.041936 -0.016135 96 Iris-versicolor
0.065834 -0.080097 -0.027612 97 Iris-versicolor
0.135344 -0.022715 0.072760 98 Iris-versicolor
-0.159894 -0.287035 -0.053823 99 Iris-versicolor
0.061480 -0.116703 -0.014806 100 Iris-versicolor
0.623664 0.115647 -0.248850 101 Iris-virginica
0.345476 -0.156399 -0.122066 102 Iris-virginica
0.618216 0.099067 0.052380 103 Iris-virginica
0.417634 -0.027520 -0.019553 104 Iris-virginica
0.563837 0.029524 -0.093273 105 Iris-virginica
0.750382 0.149908 0.159693 106 Iris-virginica
0.134786 -0.329570 -0.228790 107 Iris-virginica
0.608867 0.081795 0.186974 108 Iris-virginica
0.510127 -0.133706 0.117982 109 Iris-virginica
0.722164 0.332896 -0.110995 110 Iris-virginica
0.424673 0.113479 -0.078418 111 Iris-virginica
0.437242 -0.088411 -0.000695 112 Iris-virginica
0.541006 0.068344 -0.011776 113 Iris-virginica
0.362341 -0.242860 -0.140580 114 Iris-virginica
0.474112 -0.121029 -0.263225 115 Iris-virginica
0.514579 0.098208 -0.172265 116 Iris-virginica
0.424730 0.034656 0.005013 117 Iris-virginica
0.750875 0.461616 0.043553 118 Iris-virginica
0.871766 0.006617 0.187979 119 Iris-virginica
0.281323 -0.318538 0.088032 120 Iris-virginica
0.615417 0.152320 -0.068423 121 Iris-virginica
0.321820 -0.140376 -0.203468 122 Iris-virginica
0.757870 0.085585 0.234057 123 Iris-virginica
0.356714 -0.095280 0.000273 124 Iris-virginica
0.531812 0.167557 -0.071193 125 Iris-virginica
0.547461 0.186459 0.121773 126 Iris-virginica
0.328369 -0.068188 -0.034689 127 Iris-virginica
0.314821 -0.005581 -0.081300 128 Iris-virginica
0.516371 -0.054917 -0.062065 129 Iris-virginica
0.484863 0.114178 0.198262 130 Iris-virginica
0.632829 0.057509 0.193026 131 Iris-virginica
0.689285 0.489206 0.130646 132 Iris-virginica
0.543316 -0.055382 -0.087505 133 Iris-virginica
0.290675 -0.058369 0.064942 134 Iris-virginica
0.304493 -0.162136 0.084406 135 Iris-virginica
0.763873 0.166124 0.122873 136 Iris-virginica
0.548861 0.158169 -0.242002 137 Iris-virginica
0.406828 0.060657 -0.028793 138 Iris-virginica
0.292565 -0.016185 -0.102300 139 Iris-virginica
0.536289 0.118825 -0.007053 140 Iris-virginica
0.614381 0.091860 -0.120742 141 Iris-virginica
0.558851 0.121166 -0.061402 142 Iris-virginica
0.345476 -0.156399 -0.122066 143 Iris-virginica
0.624489 0.138445 -0.085952 144 Iris-virginica
0.639591 0.165696 -0.172950 145 Iris-virginica
0.551755 0.058990 -0.085968 146 Iris-virginica
0.406278 -0.172227 0.003916 147 Iris-virginica
0.447293 0.036996 -0.049336 148 Iris-virginica
0.489218 0.149121 -0.238719 149 Iris-virginica
0.312079 -0.031151 -0.118672 150 Iris-virginica
Apa Itu PCA (Principal Component Analysis)?#
PCA (Principal Component Analysis) adalah teknik reduksi dimensi yang digunakan untuk menyederhanakan data tanpa kehilangan informasi penting.
PCA mengubah data berdimensi tinggi (misalnya 4 fitur seperti panjang dan lebar sepal & petal) menjadi dimensi lebih rendah (misalnya 2D atau 3D), dengan:
Memproyeksikan data ke arah baru (komponen utama) yang menyimpan variasi terbesar dalam data.
Komponen utama itu adalah kombinasi dari fitur-fitur asli.
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D # Untuk plot 3D
# 1. Visualisasi PCA 2D
plt.figure(figsize=(8, 6))
for label in df_pca_2d['class'].unique():
subset = df_pca_2d[df_pca_2d['class'] == label]
plt.scatter(subset['PC1'], subset['PC2'], label=label)
plt.title("Visualisasi PCA 2D")
plt.xlabel("PC1")
plt.ylabel("PC2")
plt.legend()
plt.grid(True)
plt.show()
# 2. Visualisasi PCA 3D
fig = plt.figure(figsize=(10, 7))
ax = fig.add_subplot(111, projection='3d')
for label in df_pca_3d['class'].unique():
subset = df_pca_3d[df_pca_3d['class'] == label]
ax.scatter(subset['PC1'], subset['PC2'], subset['PC3'], label=label)
ax.set_title("Visualisasi PCA 3D")
ax.set_xlabel("PC1")
ax.set_ylabel("PC2")
ax.set_zlabel("PC3")
ax.legend()
plt.show()
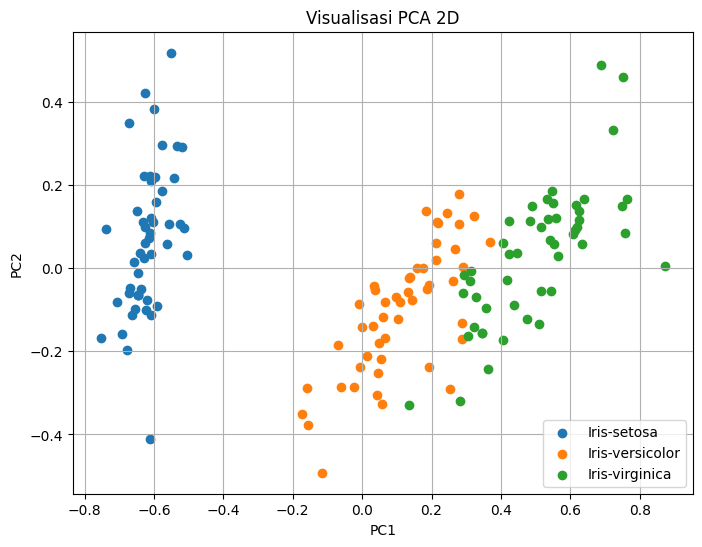
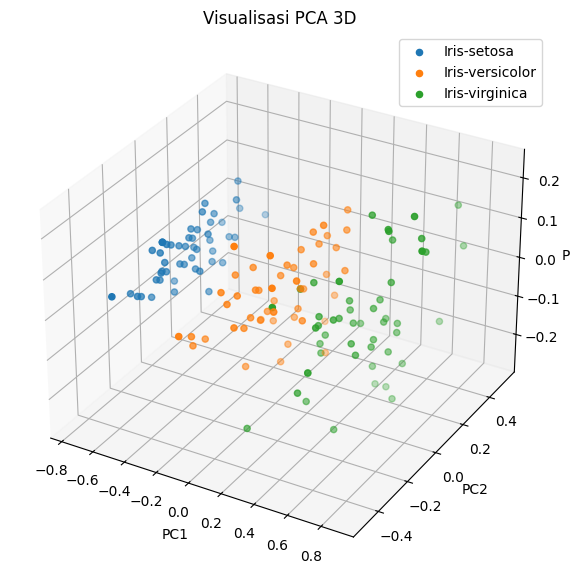
Implementasi K-Means Clustering pada Dataset Iris#
K-Means Clustering#
K-Means Clustering adalah algoritma unsupervised learning yang digunakan untuk mengelompokkan data ke dalam beberapa klaster berdasarkan kemiripan fitur.
Pada contoh ini, kita akan menggunakan dataset Iris dan menerapkan K-Means Clustering untuk mengelompokkan data menjadi 3 klaster berdasarkan fitur-fitur dalam dataset.
Langkah-langkah Implementasi#
Import pustaka yang diperlukan:
numpyuntuk manipulasi numerikmatplotlibuntuk visualisasisklearn.cluster.KMeansuntuk implementasi K-Meanssklearn.datasets.load_irisuntuk memuat dataset Irissklearn.decomposition.PCAuntuk reduksi dimensi
Load dataset Iris:
Dataset Iris terdiri dari empat fitur untuk masing-masing sampel bunga.
Fitur yang digunakan: sepal length, sepal width, petal length, petal width.
Menentukan jumlah klaster (K):
Dalam contoh ini, kita menetapkan K = 3, sesuai dengan jumlah spesies dalam dataset Iris.
Inisialisasi dan pelatihan model K-Means:
Parameter yang digunakan dalam K-Means:
n_clusters=3(jumlah klaster)init='k-means++'(strategi pemilihan centroid awal)max_iter=500(batas jumlah iterasi)tol=0.000001(toleransi konvergensi)algorithm='lloyd'(algoritma klasik untuk K-Means)
Model dilatih menggunakan
.fit(X), di manaXadalah fitur dari dataset Iris.
Mengambil hasil clustering:
kmeans.cluster_centers_: Posisi centroid setelah konvergensi.kmeans.labels_: Label klaster untuk setiap titik data dalam dataset.
Reduksi dimensi menggunakan PCA:
PCA digunakan untuk mengurangi jumlah fitur dari 4 menjadi 2, sehingga data bisa divisualisasikan dengan lebih mudah.
Transformasi dilakukan menggunakan
PCA(n_components=2).
Visualisasi hasil clustering:
Data yang telah direduksi dimensinya diplot berdasarkan label klasternya.
Centroid ditampilkan dengan simbol X berwarna hitam agar mudah dikenali.
Hasil Visualisasi#
Grafik menunjukkan pembagian klaster berdasarkan hasil K-Means Clustering.
Centroid ditandai dengan titik hitam, yang menunjukkan titik tengah dari masing-masing klaster.
Dengan PCA, kita bisa melihat bagaimana data dikelompokkan dalam ruang dua dimensi berdasarkan komponen utama.
Informasi tambahan#
Selain visualisasi, model juga mencetak:
Koordinat centroid akhir setelah iterasi K-Means selesai.
Label klaster untuk masing-masing sampel dalam dataset.
Rata-rata setiap fitur per klaster setelah proses clustering selesai.
Selanjutnya: Kita bisa mengevaluasi hasil clustering dengan Metode Elbow atau Silhouette Score untuk menentukan jumlah klaster optimal!
# Ambil hanya fitur numerik tanpa 'id' dan 'class'
X = df_merged.drop(columns=["id", "class"])
# Tentukan jumlah cluster
K = 3
# Inisialisasi K-Means
kmeans = KMeans(
n_clusters=K,
init='k-means++',
n_init='auto',
max_iter=500,
tol=0.000001,
verbose=0,
random_state=42,
copy_x=True,
algorithm='lloyd'
)
# Latih model
kmeans.fit(X)
# Ambil centroid dan label cluster
centroids = kmeans.cluster_centers_
clusters = kmeans.labels_
# Reduksi dimensi dengan PCA
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
# Visualisasi hasil clustering
plt.figure(figsize=(8, 6))
for i in range(K):
plt.scatter(
X_pca[clusters == i, 0],
X_pca[clusters == i, 1],
label=f'Cluster {i+1}'
)
plt.scatter(
pca.transform(centroids)[:, 0],
pca.transform(centroids)[:, 1],
marker='X',
c='black',
s=200,
label='Centroid'
)
plt.title("Visualisasi K-Means Clustering dengan PCA")
plt.xlabel("PC1")
plt.ylabel("PC2")
plt.legend()
plt.grid(True)
plt.show()
/home/codespace/.local/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but PCA was fitted with feature names
warnings.warn(
/home/codespace/.local/lib/python3.12/site-packages/sklearn/utils/validation.py:2739: UserWarning: X does not have valid feature names, but PCA was fitted with feature names
warnings.warn(
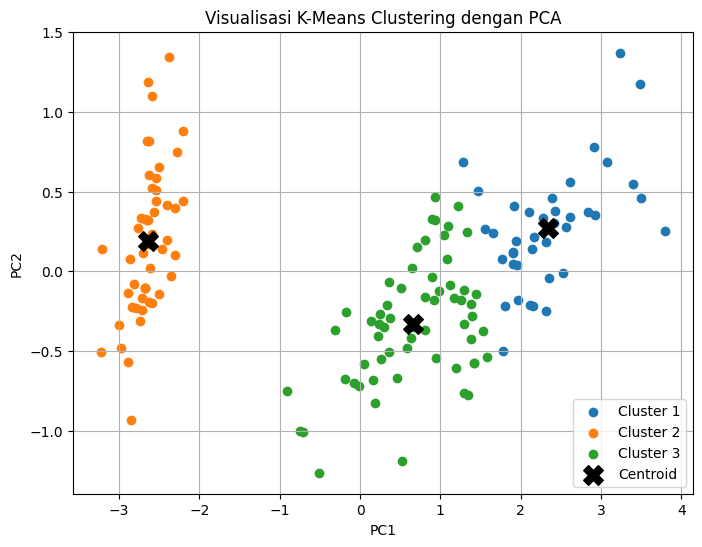
Hasil Akhir K-Means Clustering#
Berikut adalah hasil akhir dari algoritma K-Means Clustering yang telah dijalankan:
Centroid Akhir:#
Array di atas menunjukkan koordinat dari pusat (centroid) dari tiga cluster yang telah ditemukan. Setiap baris merepresentasikan satu centroid, dan setiap kolom merepresentasikan nilai rata-rata fitur untuk cluster tersebut.
Centroid 1:
[6.85384615 3.07692308 5.71538462 2.05384615]Centroid 2:
[5.006 3.428 1.462 0.246 ]Centroid 3:
[5.88360656 2.74098361 4.38852459 1.43442623]
Cluster Assignment untuk Setiap Titik Data:#
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 2 0 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 2 0 0 0 0 2 0 0 0 0 0 0 2 2 0 0 0 0 2 0 2 0 2 0 0 2 2 0 0 0 0 0 2 0 0 0 0 2 0 0 0 2 0 0 0 2 0 0 2]
Array ini menunjukkan cluster mana yang telah ditetapkan ke setiap titik data dalam dataset. Indeks array sesuai dengan indeks titik data, dan nilai pada indeks tersebut menunjukkan nomor cluster (dimulai dari 0).
1: Titik data masuk ke dalam Cluster 2.0: Titik data masuk ke dalam Cluster 1.2: Titik data masuk ke dalam Cluster 3.
Centroid Akhir per Fitur (Setiap Cluster):#
Berikut adalah nilai centroid akhir untuk setiap fitur dalam setiap cluster:
Cluster 1:
Sepal Length (cm): 6.8538
Sepal Width (cm): 3.0769
Petal Length (cm): 5.7154
Petal Width (cm): 2.0538
Cluster 2:
Sepal Length (cm): 5.0060
Sepal Width (cm): 3.4280
Petal Length (cm): 1.4620
Petal Width (cm): 0.2460
Cluster 3:
Sepal Length (cm): 5.8836
Sepal Width (cm): 2.7410
Petal Length (cm): 4.3885
Petal Width (cm): 1.4344
Interpretasi Singkat:#
Berdasarkan nilai centroid, kita dapat melihat karakteristik rata-rata dari setiap cluster. Misalnya, Cluster 2 memiliki nilai petal length dan width yang paling rendah, sementara Cluster 1 memiliki nilai petal length dan width yang paling tinggi. Cluster 3 memiliki nilai-nilai fitur yang berada di antara keduanya. Jika dataset ini adalah dataset Iris, cluster-cluster ini kemungkinan besar merepresentasikan spesies yang berbeda.
Memahami Inertia dalam K-Means Clustering#
Apa Itu Inertia?#
Inertia, juga dikenal sebagai Sum of Squared Errors (SSE), adalah metrik penting dalam K-Means Clustering yang mengukur seberapa baik data telah dikelompokkan. Semakin kecil nilai Inertia, semakin padat dan terdefinisi klaster yang terbentuk, karena titik-titik data terletak dekat dengan pusat (centroid) klaster mereka.
Rumus Inertia#
Inertia dihitung sebagai jumlah kuadrat jarak Euclidean antara setiap titik data dan pusat (centroid) klaster tempat titik data tersebut berada:
Dengan:
\(( K )\) = jumlah klaster
\(( n_i )\) = jumlah titik data dalam klaster ke-( i )
\(( x_j^{(i)} )\) = titik data ke-( j ) dalam klaster ke-( i )
\(( \mu_i )\) = pusat (centroid) dari klaster ke-( i )
\(( \| x_j^{(i)} - \mu_i \|^2 )\) = kuadrat jarak Euclidean antara titik data \(( x_j^{(i)} )\) dan centroid \(( \mu_i )\)
Peran Inertia dalam Menentukan Jumlah Klaster Optimal (K)#
Salah satu metode populer untuk menentukan jumlah klaster ( K ) yang optimal adalah Metode Elbow, yang memanfaatkan Inertia:
Hitung nilai Inertia untuk berbagai kemungkinan jumlah klaster ( K ) (misalnya, dari 1 hingga 10).
Visualisasikan nilai Inertia terhadap jumlah klaster ( K ) dalam sebuah plot garis.
Identifikasi titik pada plot di mana penurunan Inertia mulai melambat secara signifikan, membentuk визуальный “siku” (elbow). Jumlah klaster pada titik siku ini sering dianggap sebagai jumlah klaster yang optimal.
Interpretasi Nilai Inertia#
Inertia rendah: Mengindikasikan klaster yang lebih baik, di mana titik-titik data cenderung berkumpul dekat dengan centroid masing-masing.
Inertia tinggi: Menunjukkan klaster yang kurang optimal, dengan titik-titik data yang lebih tersebar jauh dari pusat klaster.
Penurunan Inertia: Umumnya terjadi dengan penambahan jumlah klaster. Namun, penambahan klaster yang berlebihan dapat menyebabkan overfitting, di mana model terlalu cocok dengan data latih dan gagal menggeneralisasi dengan baik pada data baru.
Langkah Selanjutnya: Mari kita eksplorasi implementasi Metode Elbow untuk menemukan jumlah klaster yang paling sesuai berdasarkan nilai Inertia!
# Gunakan variabel data_iris yang sudah dimiliki
X = df_merged.drop(columns=["id", "class"])
# Tentukan range jumlah cluster (K) yang diuji, mulai dari 2 sampai 10
k_range = range(2, 5)
inertias = []
# Hitung Inertia untuk tiap K
for k in k_range:
kmeans = KMeans(
n_clusters=k,
init='k-means++',
n_init='auto',
max_iter=500,
tol=0.000001,
verbose=0,
random_state=42,
copy_x=True,
algorithm='lloyd'
)
kmeans.fit(X)
inertias.append(kmeans.inertia_)
# Tampilkan nilai Inertia per K
print("Nilai Inertia per K:")
for k, inertia in zip(k_range, inertias):
print(f"K = {k}: Inertia = {inertia}")
Nilai Inertia per K:
K = 2: Inertia = 152.36870647733915
K = 3: Inertia = 78.94506582597728
K = 4: Inertia = 57.440280212954754
Penjelasan Kode: Mencari Inertia untuk K-Means Clustering#
Kode ini bertujuan untuk menghitung dan menampilkan nilai Inertia untuk berbagai jumlah klaster (K) dalam algoritma K-Means Clustering, yang diterapkan pada dataset Iris. Inertia digunakan sebagai metrik untuk mengevaluasi kualitas pengelompokan data.
Langkah-langkah:
Import Library:
numpyuntuk operasi numerik.matplotlib.pyplotuntuk visualisasi data.sklearn.cluster.KMeansuntuk algoritma K-Means.pandasuntuk manipulasi data (walaupun tidak digunakan secara eksplisit dalam kode ini).
Persiapan Data:
X = data_iris.data: Mengambil fitur-fitur dari dataset Iris dan menyimpannya dalam variabelX. Diasumsikan bahwa variabeldata_irissudah didefinisikan sebelumnya dan berisi data Iris.
Menentukan Range K:
k_range = range(2, 5): Menentukan rentang jumlah klaster (K) yang akan diuji, yaitu dari 2 hingga 4.
Menghitung Inertia:
Looping melalui setiap nilai K dalam
k_range:Membuat objek
KMeansdengan parameter yang telah ditentukan, termasuk jumlah klaster (n_clusters=k).Melatih model K-Means menggunakan data
Xdengan memanggilkmeans.fit(X).Menyimpan nilai Inertia yang diperoleh dari model (
kmeans.inertia_) ke dalam listinertias.
Menampilkan Hasil:
Mencetak judul “Nilai Inertia per K:”.
Looping melalui setiap nilai K dan Inertia yang tersimpan:
Mencetak nilai K dan Inertia yang bersesuaian dalam format yang mudah dibaca.
Tujuan:
Kode ini bertujuan untuk memberikan informasi tentang bagaimana Inertia berubah seiring dengan perubahan jumlah klaster (K). Informasi ini dapat digunakan dalam Metode Elbow untuk menentukan jumlah klaster yang optimal. Pada Metode Elbow, kita mencari titik “siku” pada plot Inertia vs. K, di mana penurunan Inertia mulai melambat secara signifikan. Titik siku ini mengindikasikan jumlah klaster yang optimal.
Catatan:
Metode Elbow: Menentukan Jumlah Cluster Optimal dalam K-Means#
Metode Elbow adalah teknik visual yang populer digunakan untuk menentukan jumlah cluster (( K )) yang optimal dalam algoritma K-Means. Ide dasarnya adalah untuk menjalankan K-Means dengan berbagai nilai ( K ) dan mengamati bagaimana metrik evaluasi (biasanya Inertia) berubah.
Cara Kerja Metode Elbow#
Latih Model K-Means dengan Berbagai Nilai ( K ): Kita melatih beberapa model K-Means, masing-masing dengan jumlah cluster yang berbeda dalam suatu rentang tertentu (misalnya, ( K ) dari 2 hingga 14).
Hitung Inertia untuk Setiap Model: Untuk setiap model yang dilatih, kita catat nilai Inertia-nya. Ingat, Inertia adalah jumlah kuadrat jarak antara setiap titik data dan centroid terdekatnya. Semakin rendah Inertia, semakin baik cluster-cluster tersebut (dalam hal kepadatan).
Plot Nilai Inertia terhadap Jumlah Cluster (( K )): Kita kemudian membuat grafik yang menunjukkan nilai Inertia pada sumbu y dan jumlah cluster (( K )) pada sumbu x.
Cari Titik “Siku” (Elbow): Bentuk grafik yang dihasilkan biasanya akan menurun seiring dengan meningkatnya jumlah cluster. Tujuannya adalah untuk mengidentifikasi titik di mana penurunan Inertia mulai melambat secara signifikan, membentuk визуальный “siku” (elbow). 拐️
Pilih ( K ) pada Titik Siku: Jumlah cluster (( K )) yang sesuai dengan titik siku ini sering dianggap sebagai jumlah cluster yang optimal. Penambahan lebih banyak cluster setelah titik ini tidak memberikan pengurangan Inertia yang substansial, yang mengindikasikan diminishing returns.
X = df_merged.drop(columns=["id", "class"])
# Tentukan range jumlah cluster yang mau diuji
k_range = range(2, 14)
inertias = []
# Hitung inertia untuk tiap K dengan parameter KMeans custom
for k in k_range:
kmeans = KMeans(
n_clusters=k,
init='k-means++',
n_init='auto',
max_iter=500,
tol=0.000001,
verbose=0,
random_state=42,
copy_x=True,
algorithm='lloyd'
)
kmeans.fit(X)
inertias.append(kmeans.inertia_)
# Tampilkan nilai inertia per K
print("Nilai Inertia per K:")
for k, inertia in zip(k_range, inertias):
print(f"K = {k}: Inertia = {inertia:.2f}")
Nilai Inertia per K:
K = 2: Inertia = 152.37
K = 3: Inertia = 78.95
K = 4: Inertia = 57.44
K = 5: Inertia = 46.54
K = 6: Inertia = 39.25
K = 7: Inertia = 35.04
K = 8: Inertia = 30.22
K = 9: Inertia = 28.76
K = 10: Inertia = 28.42
K = 11: Inertia = 27.19
K = 12: Inertia = 25.50
K = 13: Inertia = 24.08
Interpretasi Grafik Elbow#
Penurunan Curam: Bagian awal grafik biasanya menunjukkan penurunan Inertia yang curam saat kita menambahkan lebih banyak cluster. Ini karena setiap titik data menjadi lebih dekat dengan centroidnya sendiri.
Titik Siku: Titik di mana kurva mulai melandai. Ini adalah indikasi bahwa kita telah menemukan sebagian besar struktur dalam data, dan menambahkan lebih banyak cluster tidak terlalu meningkatkan model.
Penurunan Landai: Setelah titik siku, penambahan lebih banyak cluster hanya menghasilkan penurunan Inertia yang kecil. Ini bisa mengindikasikan bahwa kita mulai membagi cluster yang sebenarnya menjadi sub-cluster yang kurang bermakna.
# Plot Elbow Method
plt.figure(figsize=(8, 5))
plt.plot(k_range, inertias, marker='o', linestyle='-')
plt.title("Elbow Method - Menentukan K Optimal")
plt.xlabel("Jumlah Cluster (K)")
plt.ylabel("Inertia")
plt.grid(True)
plt.xticks(k_range)
plt.show()
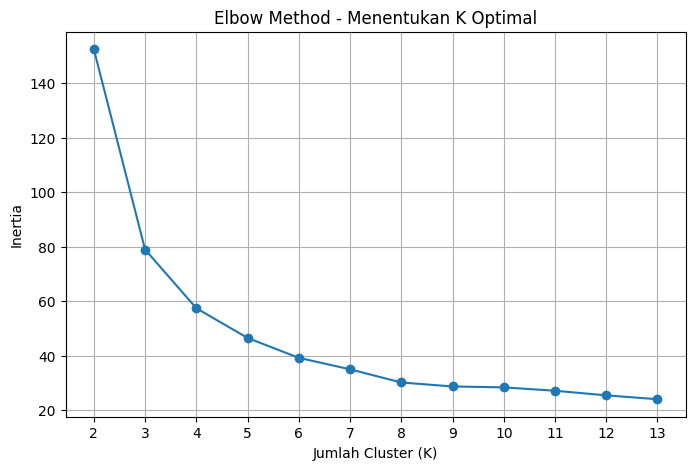
dalam hal ini Tentu, berikut adalah konten penjelasan metode Elbow yang diformat agar sesuai dengan cell Markdown di Jupyter Notebook atau Google Colab (.ipynb). Anda dapat menyalin seluruh teks di bawah ini dan menempelkannya ke dalam cell Markdown:
Markdown
Metode Elbow: Menentukan Jumlah Cluster Optimal (K) dalam K-Means (Fokus pada K=3)#
Metode Elbow adalah teknik visual yang populer digunakan untuk menentukan jumlah cluster (( K )) yang optimal dalam algoritma K-Means. Kita melatih K-Means dengan berbagai nilai ( K ) dan mengamati perubahan nilai Inertia.
Interpretasi Grafik Elbow dengan Siku di K=3#
Inertia terhadap jumlah cluster (( K )). Jika kita mengamati sebuah penurunan Inertia yang signifikan saat kita meningkatkan ( K ) dari 1 ke 2, dan kemudian penurunan yang masih cukup besar dari 2 ke 3, namun setelah ( K = 3 ), penurunan Inertia menjadi jauh lebih landai, maka kita dapat menginterpretasikannya sebagai berikut:
Dalam skenario ini, ( K = 3 ) menjadi kandidat yang kuat untuk jumlah cluster optimal. Mengapa?
Sebelum ( K = 3 ): Penambahan cluster secara substansial mengurangi Inertia, yang berarti titik-titik data menjadi lebih dekat dengan centroid cluster mereka. Struktur data yang signifikan sedang terungkap. Pada ( K = 3 ): Kita mencapai titik di mana penambahan cluster lebih lanjut tidak lagi memberikan pengurangan Inertia yang dramatis. Manfaat dari penambahan cluster tambahan mulai berkurang.
Setelah ( K = 3 ): Penurunan Inertia menjadi lebih bertahap. Ini bisa mengindikasikan bahwa kita mulai membagi cluster yang sebenarnya menjadi sub-cluster yang mungkin tidak terlalu bermakna atau hanya menangkap noise dalam data
jadi kesimpulannya data yang clusternya optimal dalam adalah k = 3
Memahami Silhouette Score dalam Clustering#
Silhouette Score adalah sebuah metrik yang digunakan untuk mengevaluasi kualitas pengelompokan (clustering) data. Metrik ini mengukur seberapa mirip suatu objek dengan cluster-nya sendiri dibandingkan dengan cluster lain. Silhouette Score memberikan nilai antara -1 dan 1, di mana nilai yang lebih tinggi menunjukkan hasil clustering yang lebih baik. 👍
Rumus Silhouette Score#
Untuk setiap titik data ( i ), Silhouette Score ( s(i) ) dihitung sebagai berikut:
Dimana:
( a(i) ) adalah rata-rata jarak intra-cluster untuk titik data ( i ). Ini adalah rata-rata jarak antara titik ( i ) dan semua titik lain dalam cluster yang sama. Semakin kecil nilai ( a(i) ), semakin baik titik ( i ) cocok dengan cluster-nya sendiri.
( b(i) ) adalah rata-rata jarak nearest-cluster untuk titik data ( i ). Ini adalah jarak rata-rata antara titik ( i ) dan semua titik dalam cluster terdekat yang berbeda dari cluster titik ( i ). Semakin besar nilai ( b(i) ), semakin baik pemisahan antara cluster.
Silhouette Score untuk seluruh clustering adalah rata-rata dari Silhouette Score untuk semua titik data dalam dataset.
Interpretasi Nilai Silhouette Score#
Catatan mengenai nilai rata-rata Silhouette Score untuk keseluruhan clustering:
Skor di atas 0.7: Dianggap sebagai indikasi clustering yang kuat, di mana cluster-cluster terpisah dengan baik.
Skor antara 0.5 dan 0.7: Dianggap sebagai clustering yang wajar.
Skor antara 0.25 dan 0.5: Dianggap sebagai clustering yang lemah, yang berarti cluster-cluster mungkin tumpang tindih.
Skor di bawah 0.25: Menunjukkan clustering yang buruk.
from sklearn.metrics import silhouette_score, silhouette_samples
X = df_merged.drop(columns=["id", "class"])
# Range jumlah cluster (K) yang diuji
k_range = range(2, 5)
silhouette_scores = []
cluster_results = {} # Simpan label dan sample silhouette untuk plotting terpisah
# Hitung Silhouette Score dan simpan hasil untuk visualisasi nanti
for k in k_range:
kmeans = KMeans(
n_clusters=k,
init='k-means++',
n_init='auto',
max_iter=500,
tol=0.000001,
verbose=0,
random_state=42,
copy_x=True,
algorithm='lloyd'
)
cluster_labels = kmeans.fit_predict(X)
score = silhouette_score(X, cluster_labels)
silhouette_scores.append(score)
print(f"K = {k}: Silhouette Score = {score:.4f}")
# Simpan hasil untuk plotting nanti
cluster_results[k] = {
'labels': cluster_labels,
'sample_silhouette_values': silhouette_samples(X, cluster_labels)
}
# ---- Silhouette Plot per Cluster ----
for k in k_range:
labels = cluster_results[k]['labels']
sample_silhouette_values = cluster_results[k]['sample_silhouette_values']
fig, ax = plt.subplots(figsize=(8, 6))
y_lower = 10
for i in range(k):
ith_cluster_silhouette_values = sample_silhouette_values[labels == i]
ith_cluster_silhouette_values.sort()
size_cluster_i = ith_cluster_silhouette_values.shape[0]
y_upper = y_lower + size_cluster_i
color = plt.cm.Spectral(float(i) / k)
ax.fill_betweenx(np.arange(y_lower, y_upper), 0, ith_cluster_silhouette_values, color=color)
ax.text(-0.05, (y_lower + y_upper) / 2, f'Cluster {i + 1}', fontsize=12)
y_lower = y_upper + 10
ax.set_title(f"Silhouette Plot for K={k}")
ax.set_xlabel("Silhouette Coefficient Values")
ax.set_ylabel("Cluster Label")
ax.axvline(x=0, color='red', linestyle='--')
plt.show()
# ---- Plot Silhouette Score per K ----
plt.figure(figsize=(8, 5))
plt.plot(k_range, silhouette_scores, marker='o', linestyle='-')
plt.title("Silhouette Score per K (Iris Dataset)")
plt.xlabel("Jumlah Cluster (K)")
plt.ylabel("Silhouette Score")
plt.grid(True)
plt.xticks(k_range)
plt.show()
# Tampilkan K optimal berdasarkan Silhouette Score tertinggi
optimal_k = k_range[np.argmax(silhouette_scores)]
print(f"\nK dengan Silhouette Score terbaik adalah: K = {optimal_k}")
K = 2: Silhouette Score = 0.6808
K = 3: Silhouette Score = 0.5510
K = 4: Silhouette Score = 0.4974
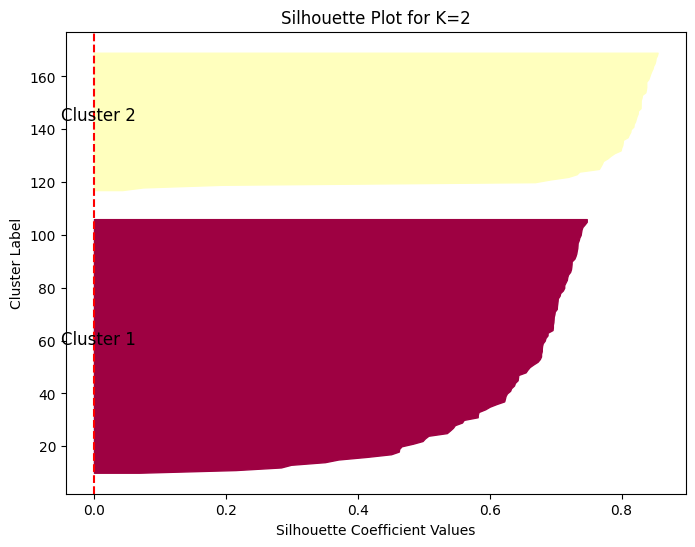
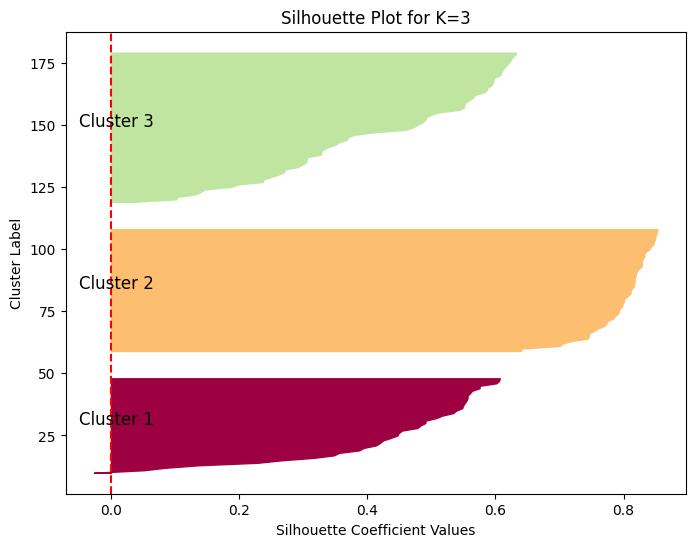
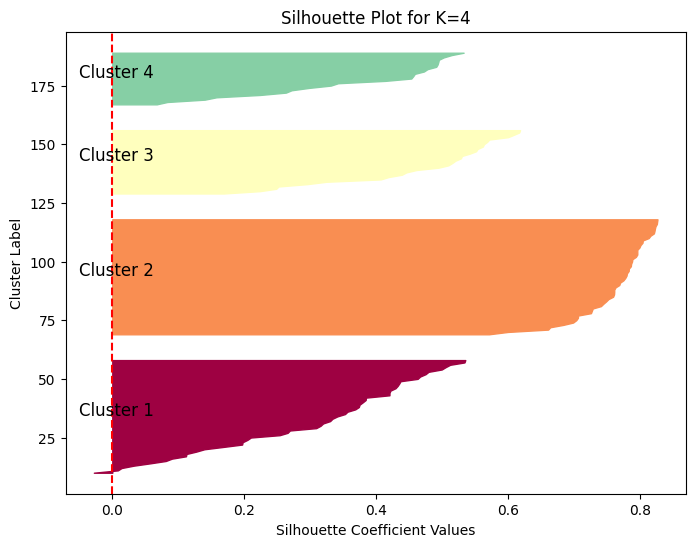
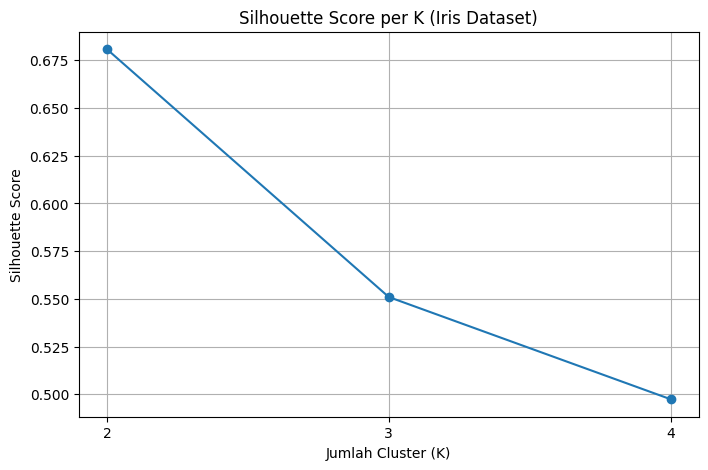
K dengan Silhouette Score terbaik adalah: K = 2
Berdasarkan hasil Silhouette Score yang Anda berikan:
K = 2: Silhouette Score = 0.6810
Nilai Silhouette Score sebesar 0.6810 untuk ( K = 2 ) menunjukkan kualitas clustering yang cukup baik hingga kuat.
Nilai ini mendekati 0.7, yang umumnya dianggap sebagai indikasi bahwa cluster-cluster terpisah dengan baik.
Sebagian besar titik data kemungkinan besar berada di dalam cluster yang tepat dan jauh dari batas keputusan antara dua cluster tersebut.
Dapat diartikan bahwa pembagian data menjadi dua cluster menghasilkan pemisahan yang jelas antar kelompok.
K = 3: Silhouette Score = 0.5512
Nilai Silhouette Score sebesar 0.5512 untuk ( K = 3 ) menunjukkan kualitas clustering yang wajar.
Skor ini lebih rendah dari saat ( K = 2 ), yang mengindikasikan bahwa menambahkan cluster ketiga mungkin membuat beberapa titik data menjadi lebih dekat dengan batas keputusan cluster lain atau cluster yang terbentuk tidak sepadat sebelumnya.
Meskipun masih di atas 0.5, ada kemungkinan beberapa titik data tidak sejelas penugasannya dibandingkan dengan kasus ( K = 2 ).
K = 4: Silhouette Score = 0.4976
Nilai Silhouette Score sebesar 0.4976 untuk ( K = 4 ) menunjukkan kualitas clustering yang lemah hingga wajar.
Penurunan lebih lanjut pada Silhouette Score ini mengisyaratkan bahwa dengan empat cluster, pemisahan antar cluster menjadi kurang jelas.
Kemungkinan ada lebih banyak titik data yang berada di dekat atau bahkan tumpang tindih dengan cluster lain.
Penambahan cluster keempat tampaknya tidak meningkatkan kualitas pemisahan secara keseluruhan dan justru cenderung memperburuknya dibandingkan dengan ( K = 2 ) dan ( K = 3 ).
Kesimpulan Sementara#
Berdasarkan nilai Silhouette Score ini, ( K = 2 ) tampaknya memberikan hasil clustering yang terbaik untuk dataset Anda (dalam hal kohesi dan pemisahan cluster) dibandingkan dengan ( K = 3 ) dan ( K = 4 ). Meskipun ( K = 3 ) masih menunjukkan clustering yang wajar, penambahan cluster menjadi 4 menghasilkan penurunan kualitas pemisahan yang lebih signifikan.
Penting untuk diingat bahwa Silhouette Score hanyalah salah satu metrik evaluasi. Pertimbangan lain seperti pemahaman domain dan hasil visualisasi (misalnya, dari Silhouette Plot individual) juga penting dalam menentukan jumlah cluster yang paling bermakna untuk data.
Penggunaan Silhouette Score dalam Praktik 🛠️#
Evaluasi Kualitas Clustering: Silhouette Score memberikan gambaran yang jelas tentang seberapa baik objek dikelompokkan. Nilai rata-rata yang lebih tinggi untuk seluruh dataset menunjukkan clustering yang lebih baik.
Memilih Jumlah Cluster Optimal: Silhouette Score juga dapat digunakan untuk membantu menentukan jumlah cluster yang optimal dalam algoritma seperti K-Means. Caranya adalah dengan menghitung Silhouette Score untuk berbagai jumlah cluster dan memilih jumlah cluster yang menghasilkan skor tertinggi.
Kelebihan Silhouette Score#
Memberikan metrik tunggal yang intuitif untuk mengevaluasi kualitas clustering.
Mempertimbangkan baik kohesi (seberapa dekat titik-titik dalam cluster) maupun pemisahan (seberapa jauh antar cluster).
Dapat memberikan wawasan tentang apakah beberapa cluster terlalu dekat atau tumpang tindih.
Kekurangan Silhouette Score#
Silhouette Score mengasumsikan bahwa cluster bersifat cembung (convex). Jika cluster memiliki bentuk yang kompleks, skor mungkin tidak mencerminkan kualitas clustering dengan baik.
Skor dapat dipengaruhi oleh kepadatan cluster. Cluster dengan kepadatan yang berbeda dapat menghasilkan skor yang tidak sebanding.
Secara keseluruhan, Silhouette Score adalah alat yang berguna untuk mengevaluasi dan membandingkan hasil dari berbagai algoritma clustering atau jumlah cluster yang berbeda. Memahami interpretasi nilainya dapat membantu dalam memilih model clustering yang paling sesuai untuk data Anda.
